Fisica per SMIA (2023/2024)
(G. D'Agostini)


 

Galleria di immagini e link associati

Misure di illuminamento

Per avere dei valori di riferimento: → Si raccomanda di usare app per farsi un'idea dell'intervallo di valori di lux
per i quali si riesce a vedere, per dirla alla buona, da 'appena appena' a 'molto bene'
Candela, lumen(*) e lux

Figura da prendere cum grano salis perché potrebbe confondere più di quanto chiarisca (scaricata da link che ora dà problemi)
 
[(*) In realtà il lumen non indica la quantità di luce ('amount of light'), coe si legge nella figura, bensì il flusso luminoso ('amount of light per unit of time'); la 'quantità di luce' è data invece dai lumen×secondo ('lm×s'), talvolta chiamato talbot (per chi fosse interessato ad approfondire e riesce a decifrare il tedesco, la voce tedesca Lumensekunde sembra più accurata)]
Simpatiche analogie fra flusso luminoso e flusso di acqua (e grandezze correlate)
 
    
Energia potenziale in Aula Picone per un oggetto di 1 kg...
 
... prendendo Ep = 0 ↠ La Fisica non cambia!
Energia potenziale gravitazionale per una massa di 1 kg
dalla superficie della Terra all'infinito.
 

(Distanza dal centro della Terra in unità del raggio terrestre)
 
Notare l'andamento pressoché lineare per r/RT poco superiore a 1
(ovvero nell'intorno della superficie terrestre): → raccordo con 'mgh'.
Spettro elettromagnetico
Corrispondenza fra lunghezza d'onda e colori.
Pendolo interrotto di Galileo:
  diminuzione di quota → aumento di velocità;
  diminuzione di velocità → aumento di quota;
  etc. etc. ...

[Cliccare per vedere dimostrazione e spiegazione]
Altro video
Mulinello di Joule
[Altre risorse in rete]
Potere calorifico dei vari combustibili
Dettaglio di una busta di pellet.

 
Esercizio: → convertire il valore in MJ/kg
[ovviamente ci sono siti che lo fanno, da usare solo per eventuale controllo]
 
Per capire la convenienza dei vari combustibili bisogna tener conto del potere calorifico (riportato in MJ/kg, in kWh/kg o in kcal/kg),
del prezzo al chilogrammo, del costo dell'impiano, della comodità di esercizio, etc. etc.
Diga di Castel Giubileo
 
Esercizio: ricavarsi la potenza erogata dai dati e assumendo
una efficienza di conversione da energia meccanica a energia elettrica quasi unitaria.
Potenza dei ciclisti nello sprint di arrivo (!!)
Piano inclinato e piste arcuate
Si immaginino tre punti materiali che scivolano senza attrito lungo le guide(*)
rappresentate in figura, partendo allo stesso istante con velocità nulla.
Quello blue è un normale piano inclinato, mentre gli altri due sono arcuati.
[(*) Nota: i due archi di cerchi non sono speculari rispetto alla linea del piano inclinato
perché altrimenti quello verde avrebbe pendenza nulla in x=0 e il punto materiale resterebbe lì fermo
(anche se si tratta di equilibrio instabile). Il centro di tale cerchio è in (-0.2,-0.2).]
E se fosse caduto verticalmente?
Energia potenziale, lavoro eseguito dalla forza peso e energia cinetica finale
 
Giro della morte
 
Video interessante (finché parla del giro della morte, poi si perde con cose ad effetto che non vengono spiegate) che però non giustifica la ragione per cui la forza centripeta nel punto più in alto debba essere maggiore di mg. Il motivo è perché ci deve essere anche una reazione vincolare della guida, senza la quale viene meno la condizione di contatto.
Tipica utilizzazione di piani inclinati (*)
[Foto da qui]
 
[(*) L'idea chiave è che lo stesso lavoro può essere compiuto giocando sulle variabili 'forza' e 'spostamento']
Uso della leva per 'moltiplicare la forza' (*)
 

"δός μοι ποῦ στῶ καὶ κινῶ τὴν γήν."
 
 
[(*) L'idea chiave è che lo stesso lavoro può essere compiuto giocando sulle variabili 'forza' e 'spostamento']
Uso di sistemi di carrucole per `moltiplicare la forza' (*)
 

 
[  Da Wikipedia: si notino i rapporti di moltiplicazione e gli spostamenti degli estremi ]
 
[(*) L'idea chiave è che lo stesso lavoro può essere compiuto giocando sulle variabili 'forza' e 'spostamento']
Curve P-V per diverse temperature ('isoterme')
[Applicazione dell'equazione di stato dei gas perfetti]
 

 
Scale lineari e logaritmiche
applicate alle curve del test di autovalutazione
 
 
Finalmente non si sono dubbi su quali sia, a occhio, l'andamento esponenziale.
Script R (conversione in Python opzionale):
Andamenti esponenziali crescenti
    
Ricorda qualcosa? (anche numericamente)
Tacchino esponenziale
→ m(t) e v(t) in scale normali e logaritmiche
Script R: tacchino_l.R
Processo di termalizzazione

Script R:
Velocità limite nel caso di forza costante + forza di attrito del tipo -βv
 
Script R: v_resistenza_mezzo_anim.R
Spettacolare passaggio di Pasqua della Stazione orbitale
(peccato il cielo sabbioso, ma si è vista...)
 

 
[ Previsione di Astroviewer ]

Traccia e dettagli prevista 5 giorni prima da ISS Detector
A proposito di scale logaritmiche
(Da TOP500 — il nr. 6 è Italiano)
    GFLOPS

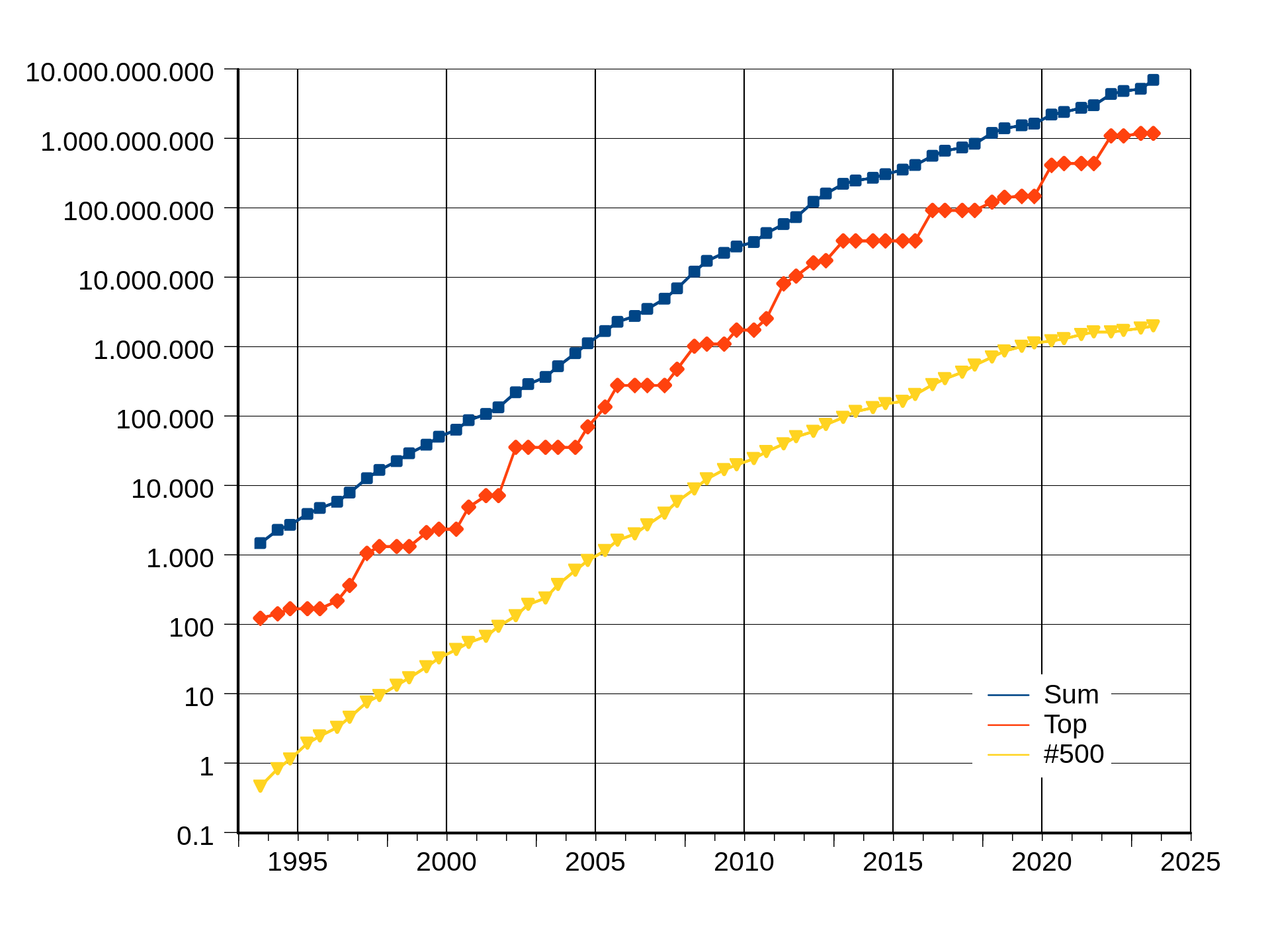
[ Trend dei sistemi operativi usati nei TOP500 ]
 
Che legge segue, approssimativamente, la potenza di calcolo in funzione del tempo?
Volume uovo di polistirolo
Per 'riprodurre' grafica e calcoli Nota: il metodo usato è un po' 'casereccio'. Un modo più professionale per affrontare il problema
è quello 'scandagliare' i pixel dell'immagine per trovare il contorno dell'uovo dalla transizione 'bianco'/'rosso'.
Uso di un tubo a U per la misura della sovrapressione all'interno di un palloncino
 
 
[Vedi anche tubo manometrico su Wiki]
Pressione
Forze di pressione all'interno di un fluido
Paradosso idrostatico
           
La pressione dipende solo dal livello di acqua
e non dalla quantità d'acqua (o altro fluido) contenuto nel recipiente.
→ Talmente controintuitivo da essere noto come paradosso.
Pressione nei fluidi
Vasi comunicanti
Prima osservazione del vuoto (di poco antecedente a quella di Torricelli)

(Esperimento di Gasparo Berti, Roma c.a 1642)
Perché un liquido sale in una cannuccia...
 
A proposito di Glashow: From Alchemy to quarks
Emisferi di Magdeburgo
[Video]
Analisi lanci orizzontali
1. Equazioni orarie
2. Traiettorie
3. Velocità (in modulo)
4. Velocità estesa a 1 s (si immagini il tavolo posto su un balcone)
Epitaffio di Stevino e visualizzazione grafica delle forze in gioco
(Cosa significa avere idee geniali!)
 
[Masse proporzionali alle lunghezze dei cateti e collegate fra loro
da una corda sono in equilibrio (le frecce rosse sono uguali in modulo)
il tratto di catena che penzola sotto l'ipotenusa è irrilevante!]
Analisi affondamenti cilindri (→ dati)
↠ Valutare i coefficienti di linearità m1 e m2
Rette per due punti
Script R: rette_2p_live.R
Distanza vs periodo dei pianeti del sistema solare
(Vedi dati_pianeti.txt, da nasa.gov)
1. plot 'normale'
('R_T' sta per il raggio dell'orbita terrestre, in approssimazione circolare
'y' sta per per l'anno solare terrestre.)
 
2. plot linearizzato 'seguendo Keplero'
3. plot linearizzato mediante scale logaritmiche
(vedi anche plot si Wikipedia riportato sotto)
Script R: pianeti_overview.R, pianeti_log.R
Script Python: pianeti_log.py
Linearizzazione dati affondamenti mediante scale log-log
(Per i dati e il plot in scala 'normale' vedi sotto)
 
Script R: affondamenti_log.R (→ convertire in Python)
Equinozio di primavera
 
In Rome, Italy: Wednesday, 20 March 2024, 04:06 CET
Spettacolari sorgere di Luna e transito della ISS davanti alla Luna(*)
 

 
 
(*) Quale dei due è realistico e quale è una bufala?
 
Oscillazione di un pendolo semplice
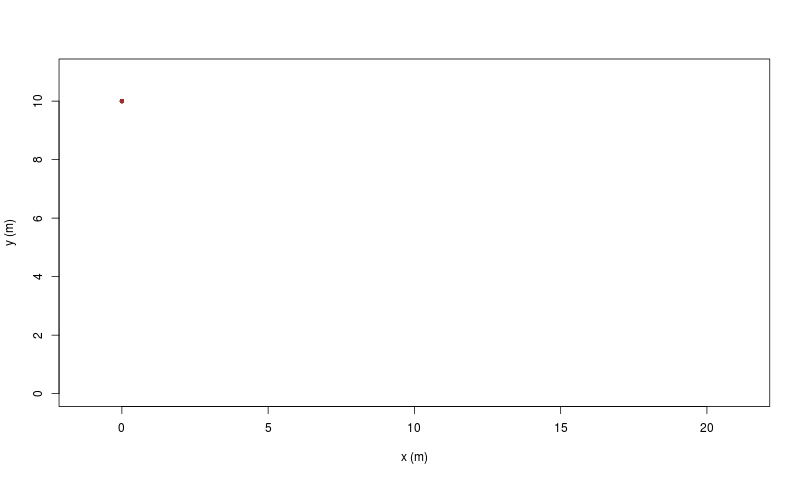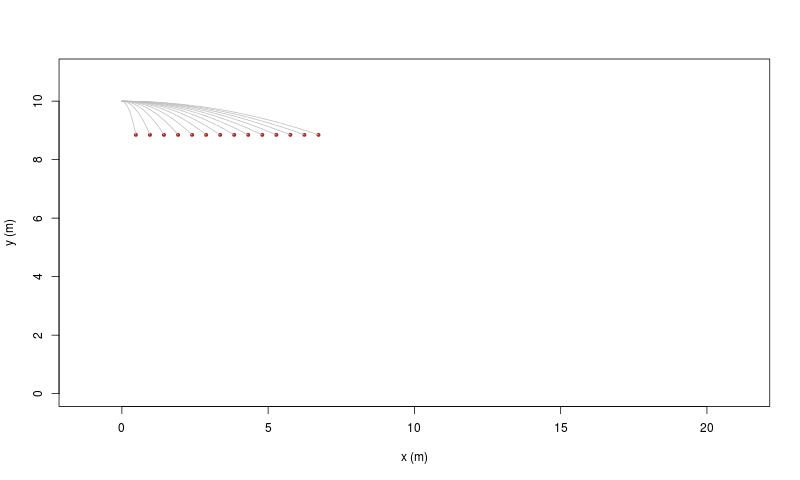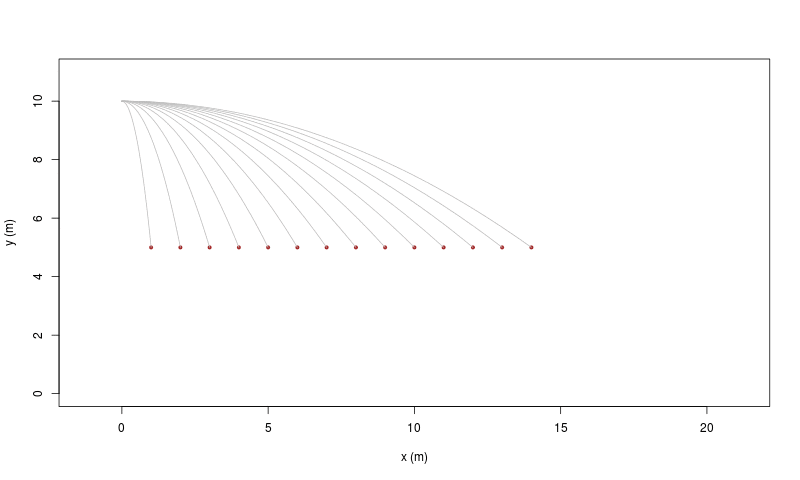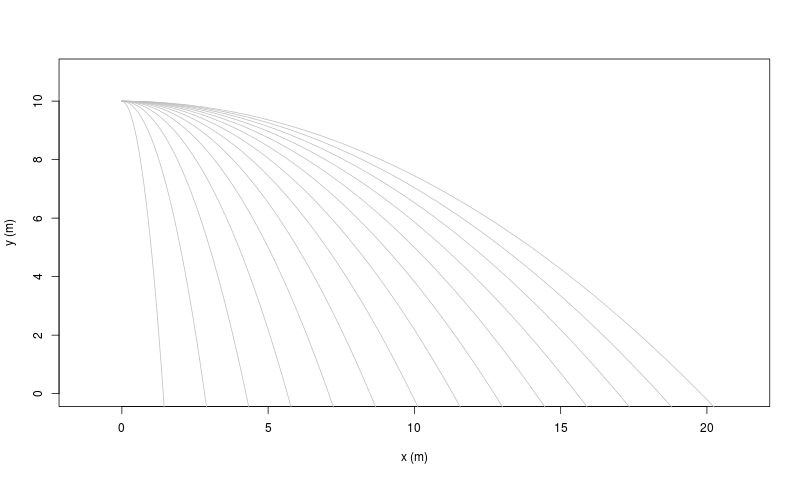
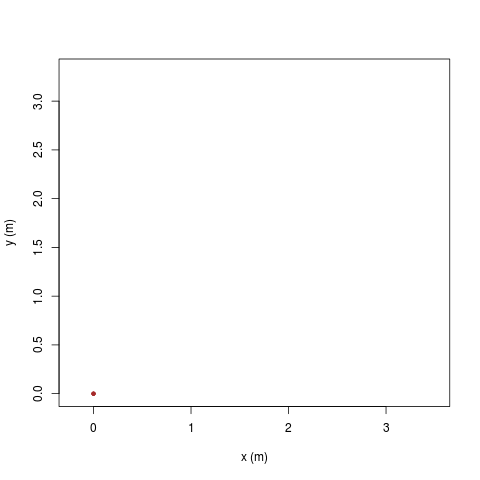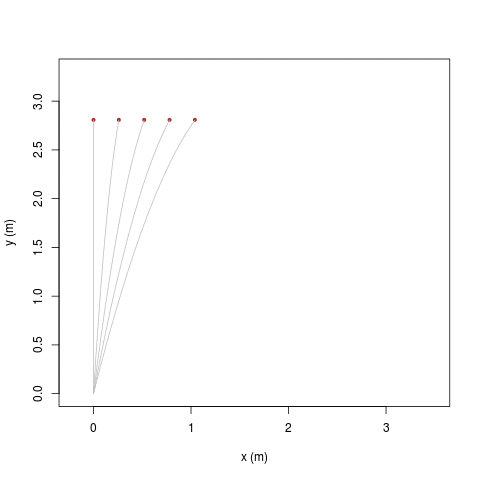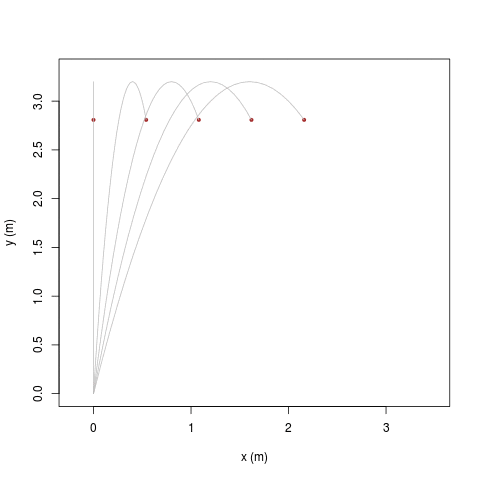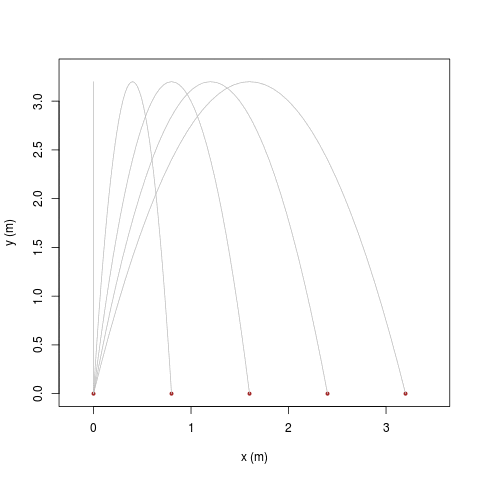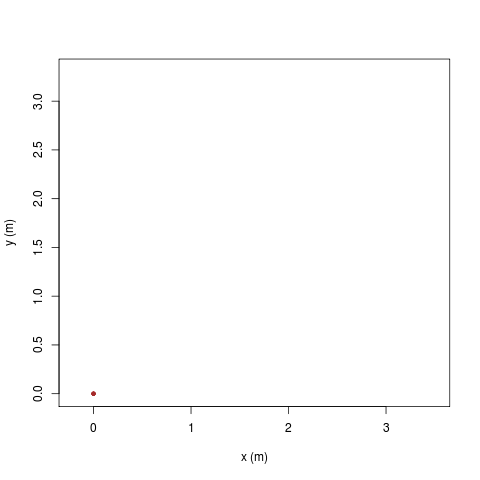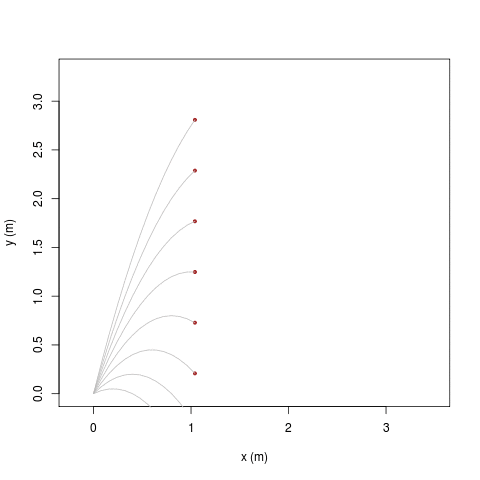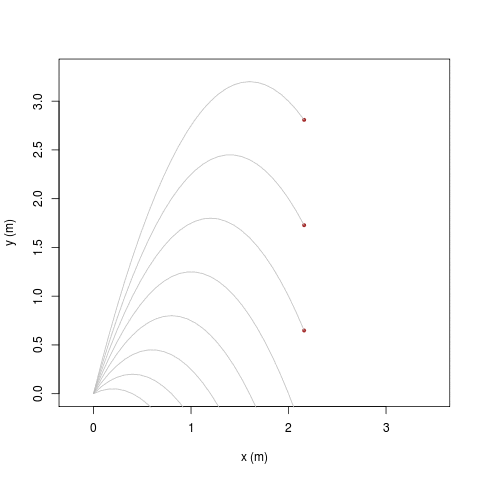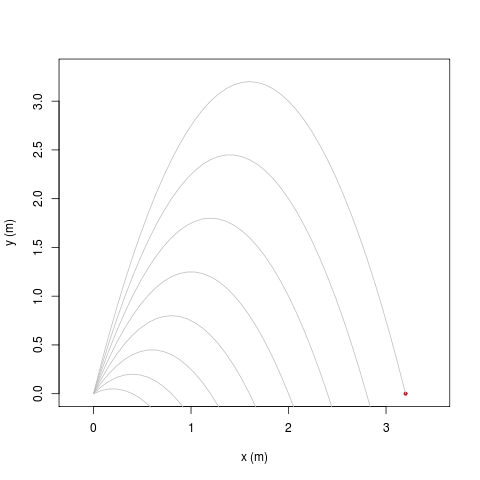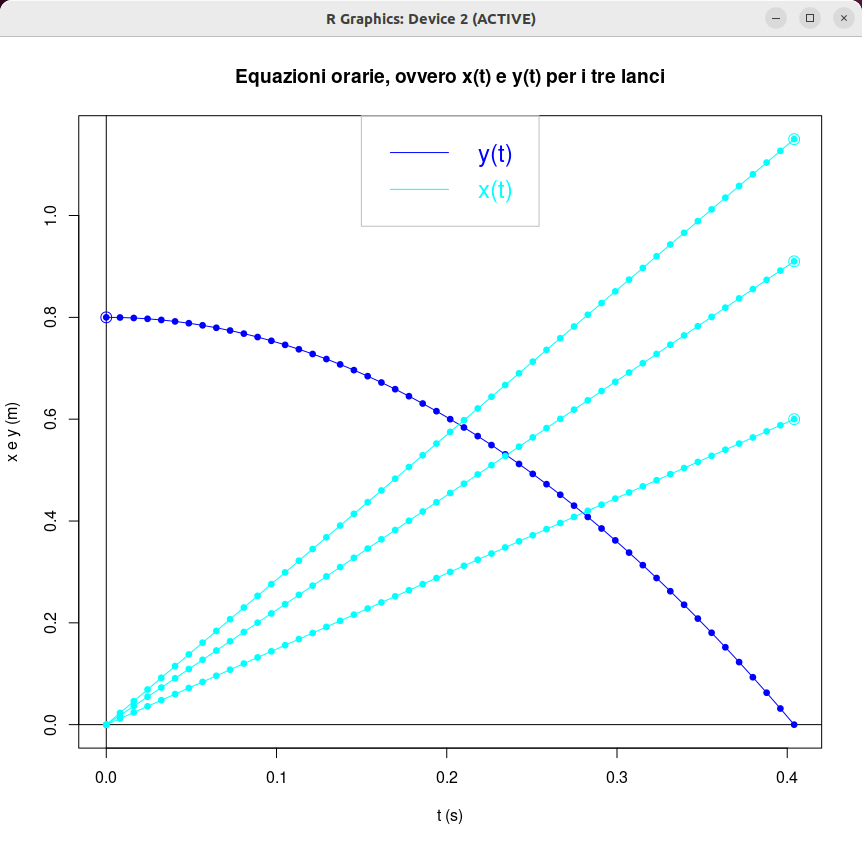
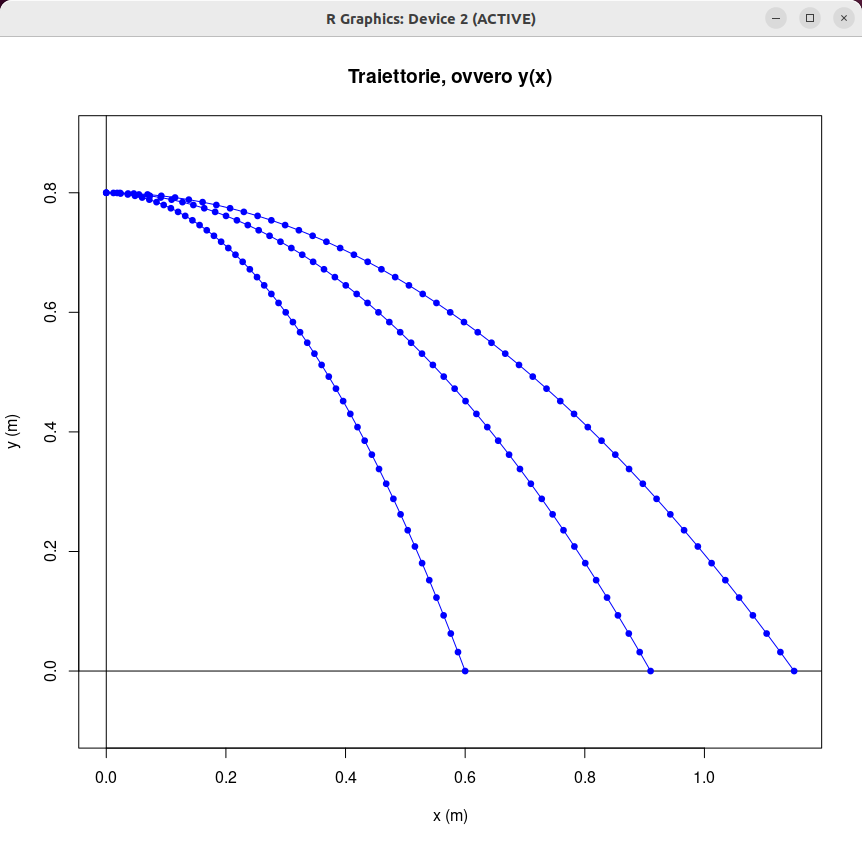
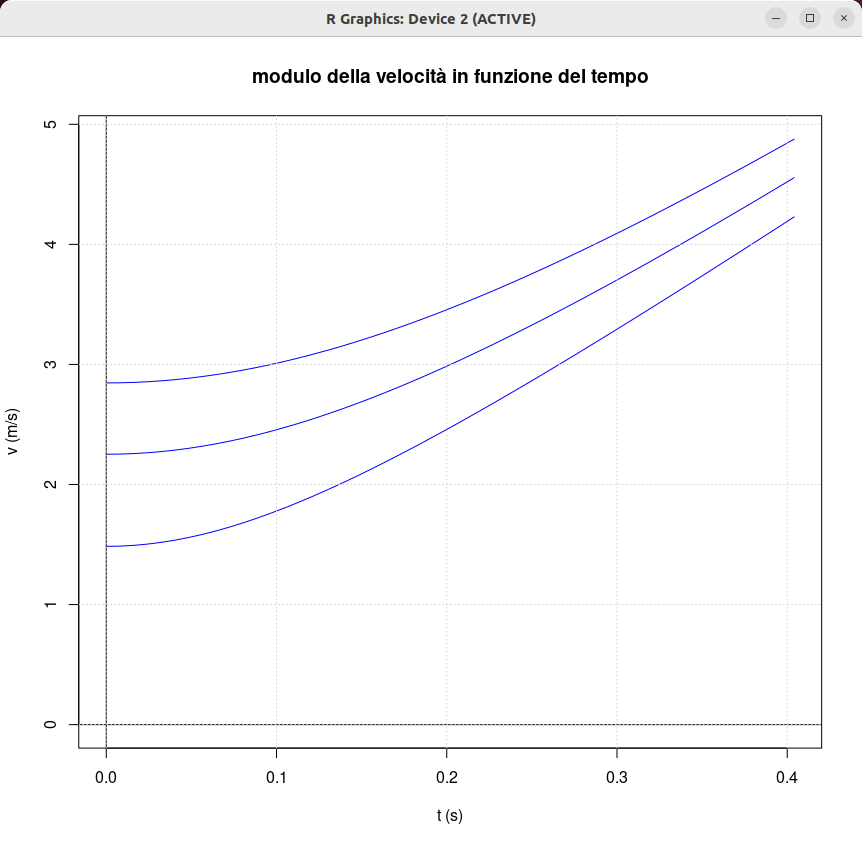
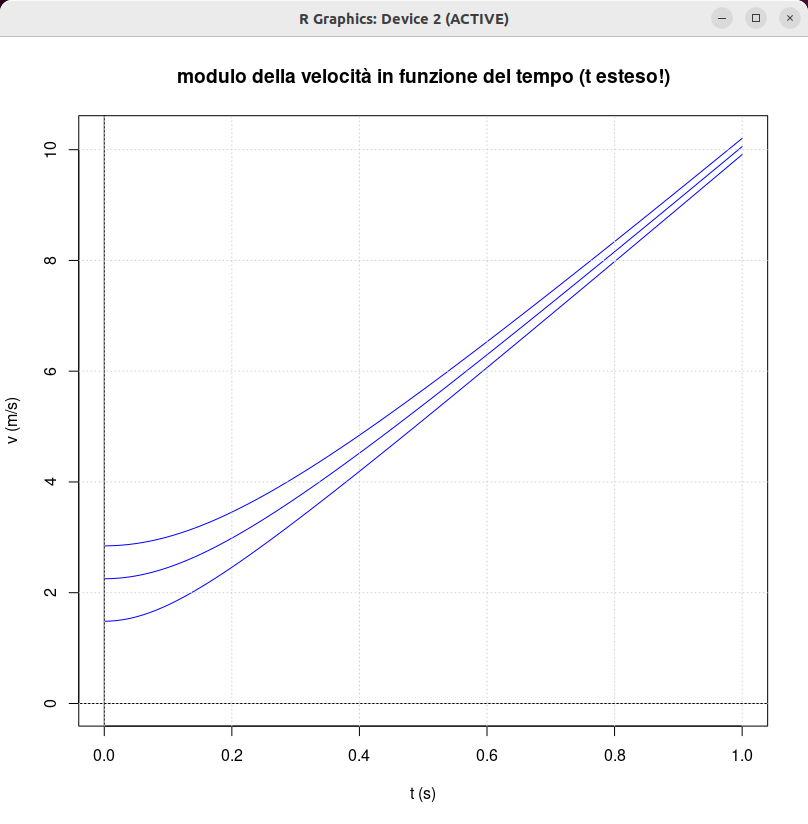
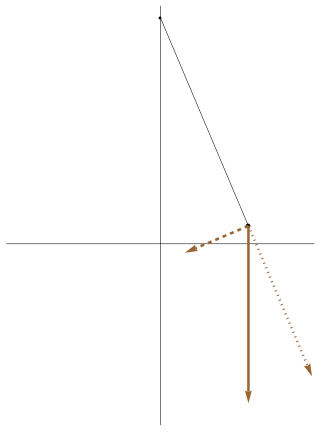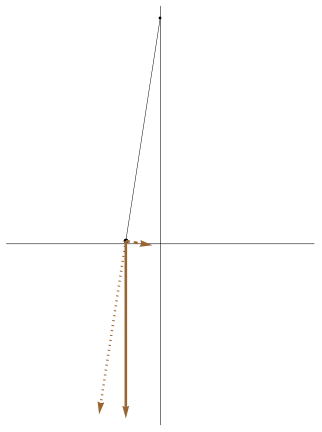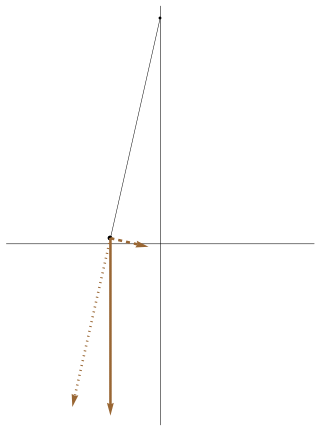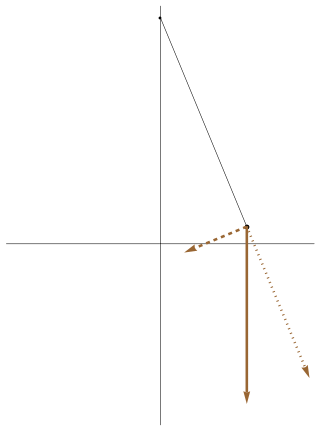
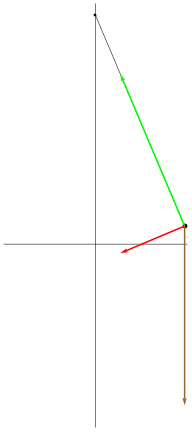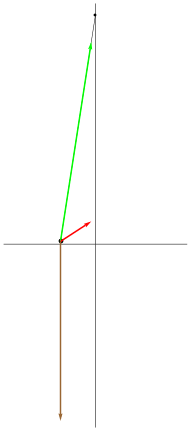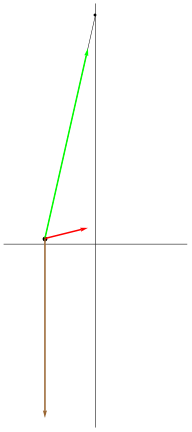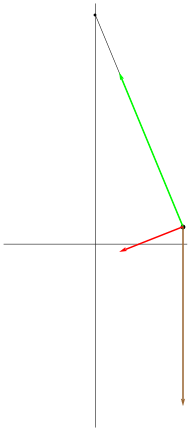
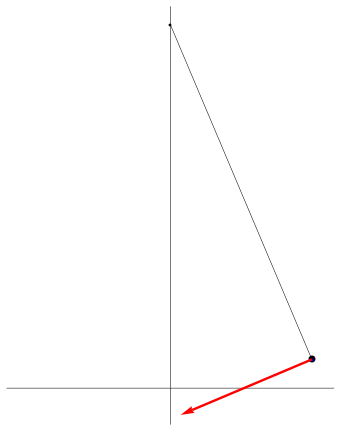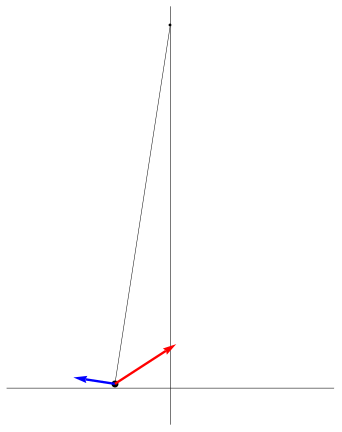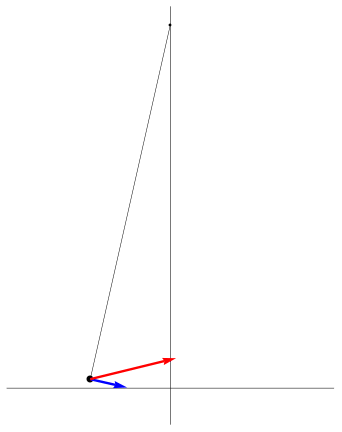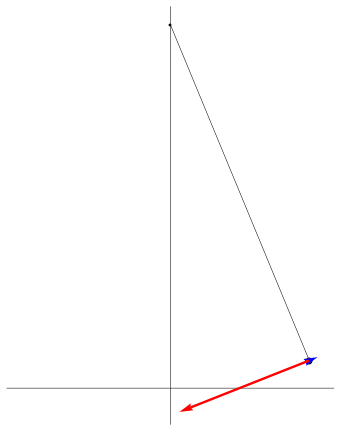
Moto del pendolo: componenti tangenziale e normale della forza di gravita'           Moto del pendolo: forza di gravita' (marrone), del filo (verde) e totale (rosso) in funzione del tempo           Moto del pendolo: vettori velocita' (blu) e accelerazione (rosso) in funzione del tempo
 
Cosa rappresentano le varie frecce? È importante per 'capire' le formule (invece di impararle a memoria)
In particolare:
  → identificare le frecce che visualizzano velocità e accelerazione
  → e confrontarle con il caso di moto circolare uniforme e uniformemente accelerato.
Quantità di calore fornito e variazione di temperatura (o transizione di fase, a T costante)  

[ Da Wikipedia. Attenzione: i tre 'c' sono numericamente diversi, come si evince dalle diverse pendenze,
mentre i vari λ non sono calori latenti, bensì calori latenti specifici (vedi e.g. 'SLH' in en.wikipedia) ]
 
 
Per capire la difficoltà pratica per definire una scala ufficiale di temperature vedi la Scala Internazione di Temperature del 1990, e in particolare le tabelle (Niente a che vedere con metro, chilogrammo e secondo!)
 
Si fa presto a dire termometro...
(sempre a proposito di principio di misura)
 
(+ termoresistenze, sensori di temperatura a diodo etc.)
Letture raccomandate
(a proposito delle misure di longitudine e latitudine)
 
     
 
Raro arcobaleno verso nord
 

 
[Arcobaleno alle 9:27 del 7 dicembre 2020 - Particolare sul palazzo in costruzione]
 
Come si fa a capire che la foto è stata scattata (circa) verso nord?
Lanci orizzontali
(in prossimità della superficie terrestre, trascurando la resistenza dell'aria)
 
Casi particolari di lanci
(in prossimità della superficie terrestre, trascurando la resistenza dell'aria)
[ stessa vy0;   diverse vx0 ] [ stessa vx0;   diverse vy0 ]

 
→ Indipendenza dei moti sui due assi cartesiani.
Lanci in funzione dell'angolo rispetto al piano orizzontale
Proiettili lanciati nello stesso istante con stessa velocità in modulo ma diversa angolazione. La traiettoria indicata in rosso corrisponde a 45 gradi.
 
Oggetto sospeso a molla, allontanato dal punto di equilbrio
(la tensione dell'elastico ci dà un'idea della forza applicata, e quindi della forza di richiamo(*) della molla).
 
   
 
[(*) Questa non va confusa con la forza totale esercitata dalla molla ]
Funzioni sinusoidali e loro derivate
[(*) Si ricorda che la derivata rispetto al tempo di una grandezza fisica dà luogo a una grandezza fisica
avente dimensioni diverse di quella di partenza, come ci ricorda la notazione di Leibniz delle derivate.
→ Vedi sulla 'mostruosità' di disegnare sullo stesso piano vettori rappresentanti diverse grandezze fisiche!]
Ricordarsi della stazione orbitale
Resistenza dell'aria
Effetto dell'aria sulla caduta dei gravi
 
1. Esperimento in laboratorio (→ video)
   
 
 
2. Esperimento sulla Luna (→ video)
Forza di attrito statico
 
Valutare l'ordine di grandezza della forza di attrito statico esercitata su ciascun arto.
Misura del coefficiente di attrito statico
[Buon uso didattico di un laptop... ]
Riproduzione scolastica del piano inclinato con i campanelli di Galileo Galilei
 
Mix di piano inclinato (possibilmente con attrito) e carrucola
 
 
[Come si può ben capire, la combinazione può dar luogo a una varietà di problemi:
  importante aver capito lo schema concettuale da usare, senza (tentare di) imparare a memoria tutta la casistica.]
Pesa più un pallone sgonfio o un pallone gonfio?
[Nel senso se indica di più su una bilancia — per la serie del "kg di piombo e del kg di paglia"]
 

??
??
Passaggio luminosissimo della stazione orbitale ISS giovedi 14 marzo
[Passaggi molto luminosi anche venerdi 15 e domenica 17 (meteo permettendo...)
e in entrambi i casi, c.a 1h28' dopo quello molto luminoso ne segue un secondo
ancora visibile, anche se meno luminoso (ecco ad es. venerdi).]
 

 

 

[→ Magnitude -4.7 !]
 
App Android usata (ma ce ne sono altre, anche per altri sistemi operativi)
Alcuni siti che danno la posizione attuale e le previsioni dei passaggi visibili:
- ISS.AstroViewer [previsione di giovedi 14 marzo]
- ISS Tracker
Dal "cannone di Newton" alla derivazione di Feynman della velocità di un corpo in orbita circolare
 
       
 
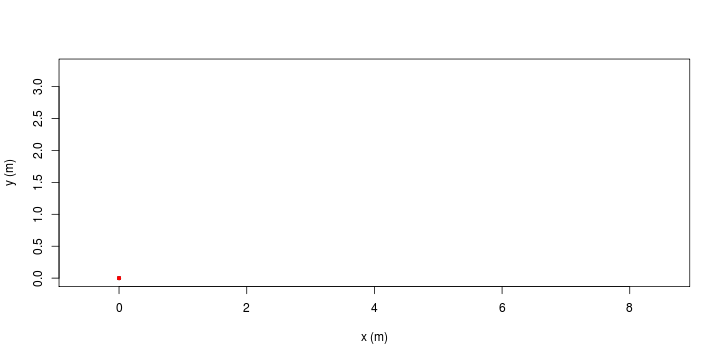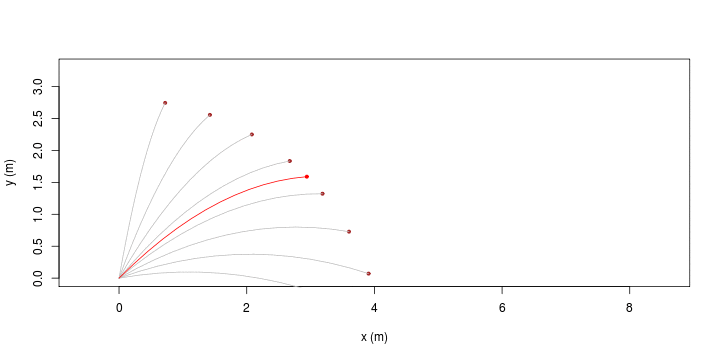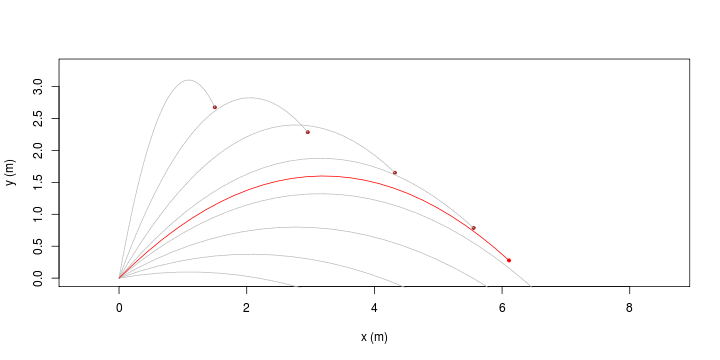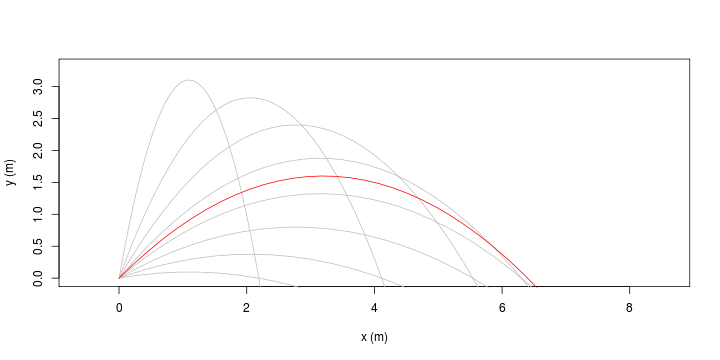
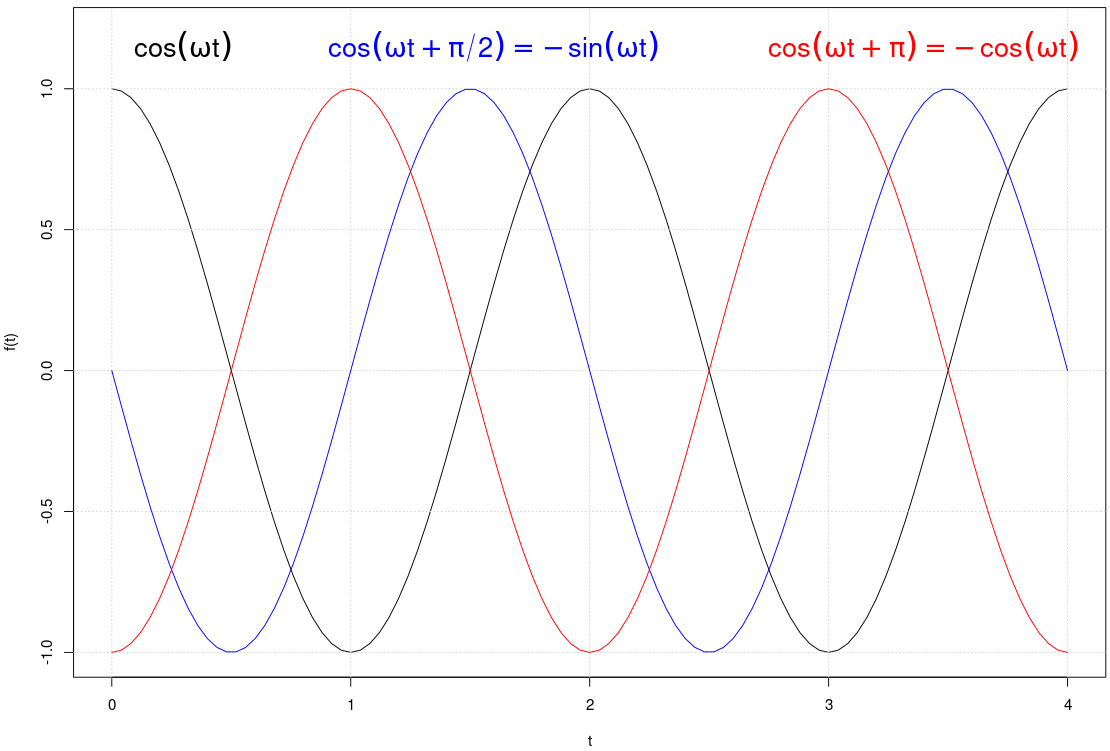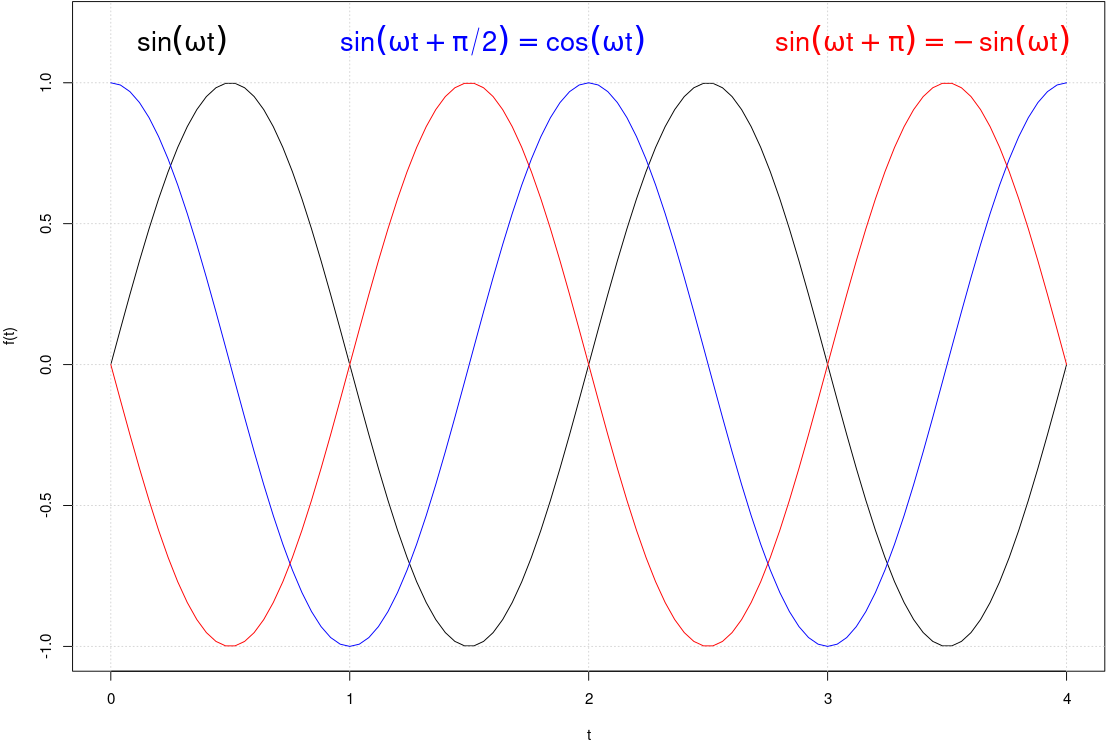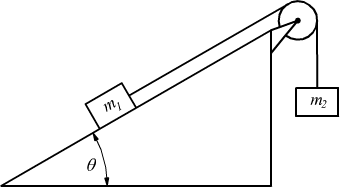
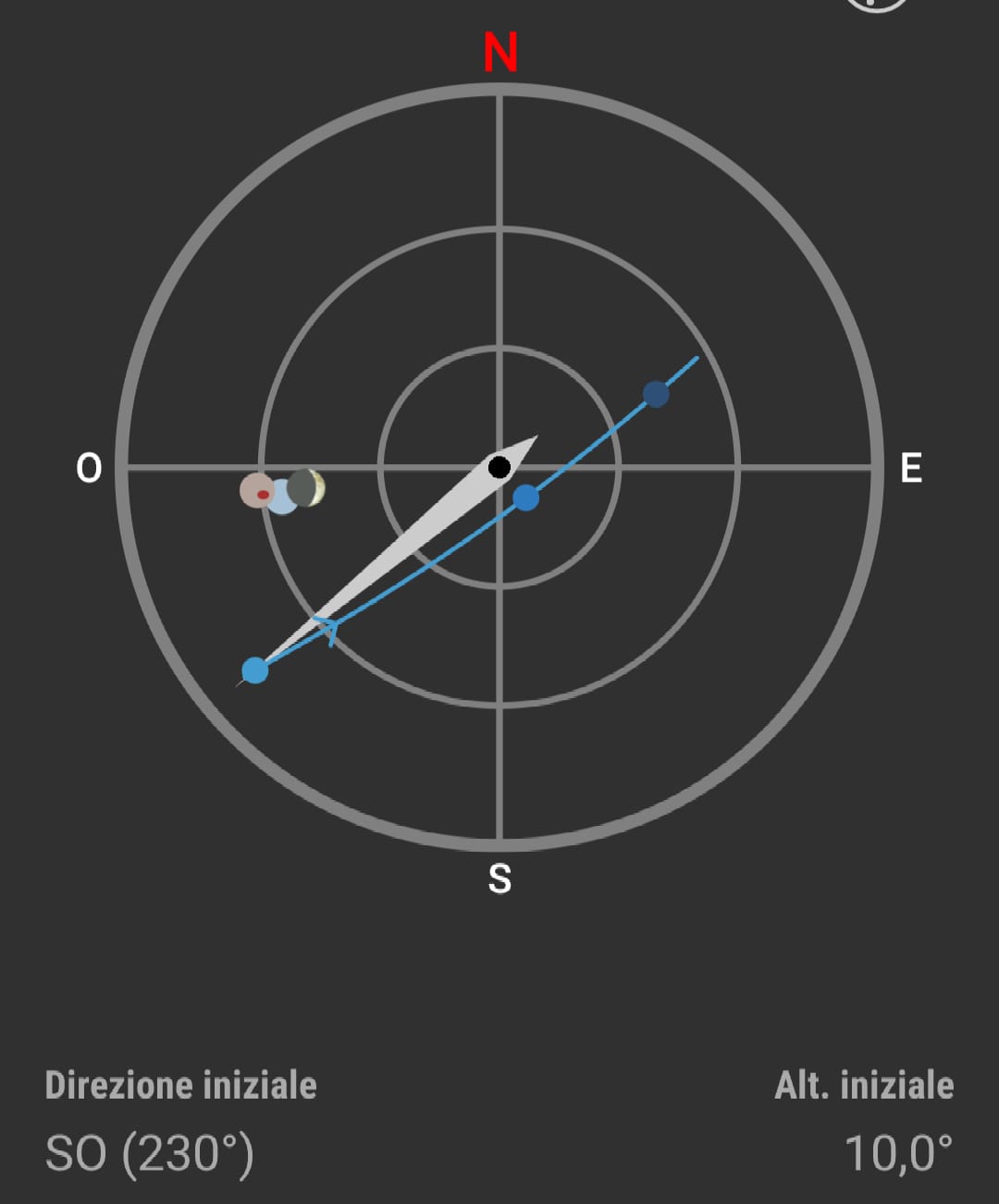
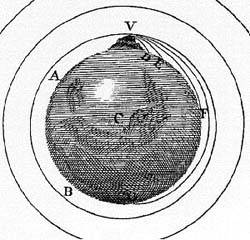
[ vedi sotto ]
 
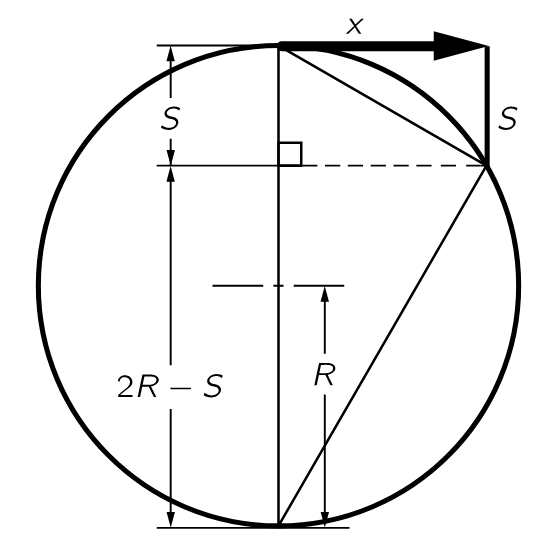
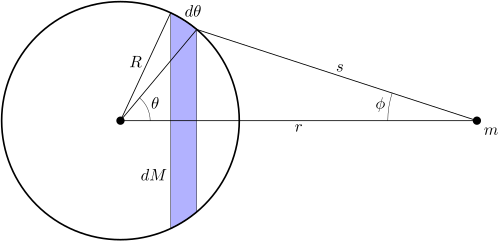
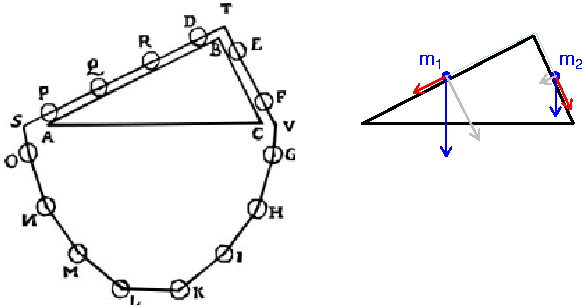
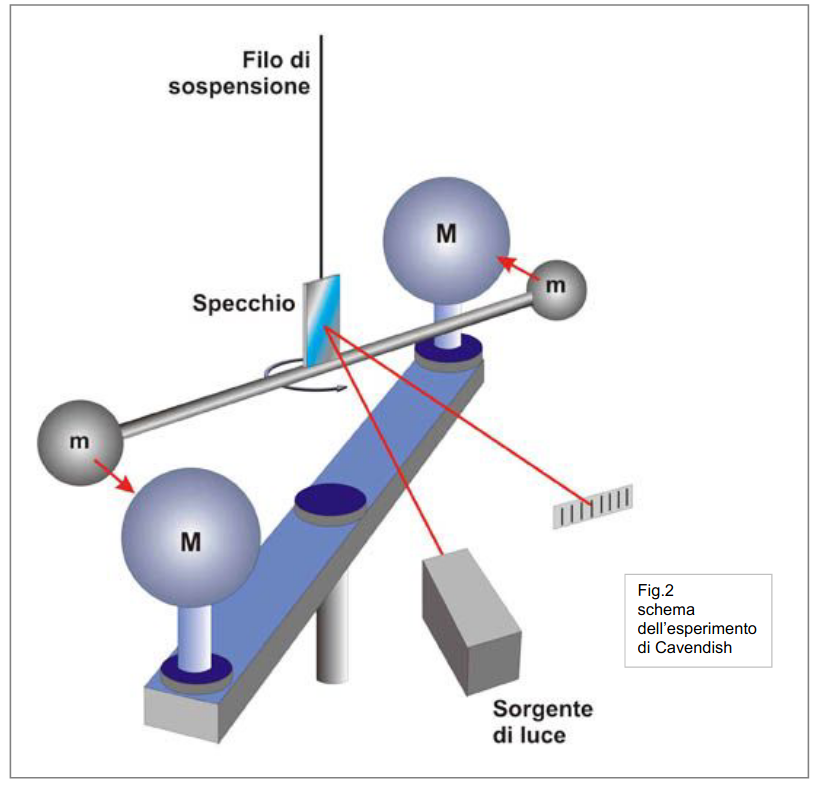
[ da La Fisica di Feynman, Sec. 7.4 ]
 
Nota: il grosso triangolo rettangolo di destra è fortemente esagerato, per renderlo visibile graficamente.
 
Ragionamento (ove in figura 'R' sta ovviamente per RT): → Ricavarsi, come esercizio i valori di v per
  1. l'ipotetica orbita radente intorno alla Terra;
  2. la Stazione Orbitale (con 'gISS');
  3. la Luna (con 'gLuna').
[Una volta ricavata la velocità ci si ricava facilmente il periodo.]
Apparatus for showing the independence of vertical and horizontal motions (*)
(Sempre dallo stesso capitolo del primo volume de La Fisica di Feynman)
 
Se allo stesso istante le due palline hanno velocità nulla,
cadranno dello stesso spazio nello stesso tempo.
[Ma l'urto si verifica se
  1. le distanze orizzontali e l'altezza da cui viene lasciata rotolare
    la pallina di destra vengono scelte in modo opportuno;
  2. si riesce a sincronizzare il rilascio della pallina di sinistra
    con l'istante in cui quella di destra lascia la guida.]
(*) La questione è legata al 'famoso' problema de La scimmia e il cacciatore
(anche se, come al solito, rendono il problema più lungo e complicato di quanto necessario...)

Terza legge di Keplero applicata ai pianeti del Sistema Solare (immagine da Wiki)

Corpi orbitanti intorno alla Terra  

[ Colpo d'occhio su alcuni parametri orbitali (da Wikipedia) − Nota: le orbite reali non sono coplanari!(*) ]
 
(*) Solo i satelliti geostazionari hanno l'orbita sul piano equatoriale,
come mostrato invece nella figura al fine di confrontare i vari parametri.
Le dimensioni della Terra (palesemente vista dal Polo Nord) e delle varie orbite sono in scala(!).
Le quattro scale mostrano i parametri orbitali in funzione della distanza dalla Terra ('Mm' sta per 106m, ovvero 1000 km).

[ Rotazione della Terra e di un satellite geostazionario (da Wikipedia − vedi anche qui) ]
Vecchia foto per ricordare i tipi di solidi affondati
(cilindro, cono e prisma)
In particolare, si notino le tacche sul prisma di marmo, a ricordare
che esso viene affondato (dalla punta) con tale lato ortogonale alla superficie dell'acqua.
 
Esperimenti non eseguiti in aula (in questo corso):
- la cosa più interessante e più istruttiva è la loro analisi!
- dati simulati: dati_affondamenti.dat , ove
    'x' indica l'affondamento 'nominale' in centimetri;
    dm1, dm2, dm3 e dm4 rappresentano le variazioni delle letture sulla bilancia;
    (per il loro significato vedi figura subito sotto)
 
Visualizzazione grafica dei dati raccolti:
 
Nota: i segmenti che uniscono i punti non hanno alcun significato statistico/inferenziale.
Sono solo, come si dice, "to guide the eye".
Spinta di Archimede dell'aria
→ a proposito della misura della massa del polistirolo
     
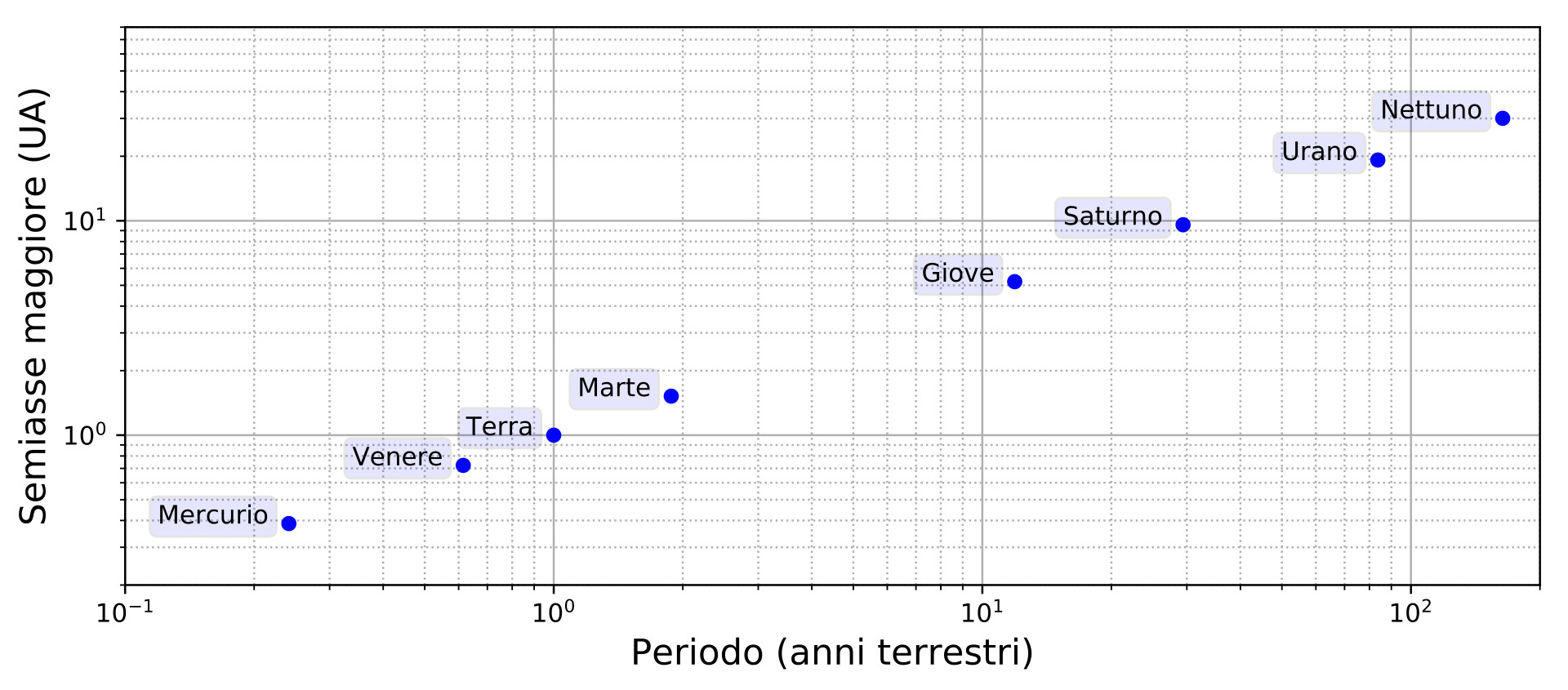
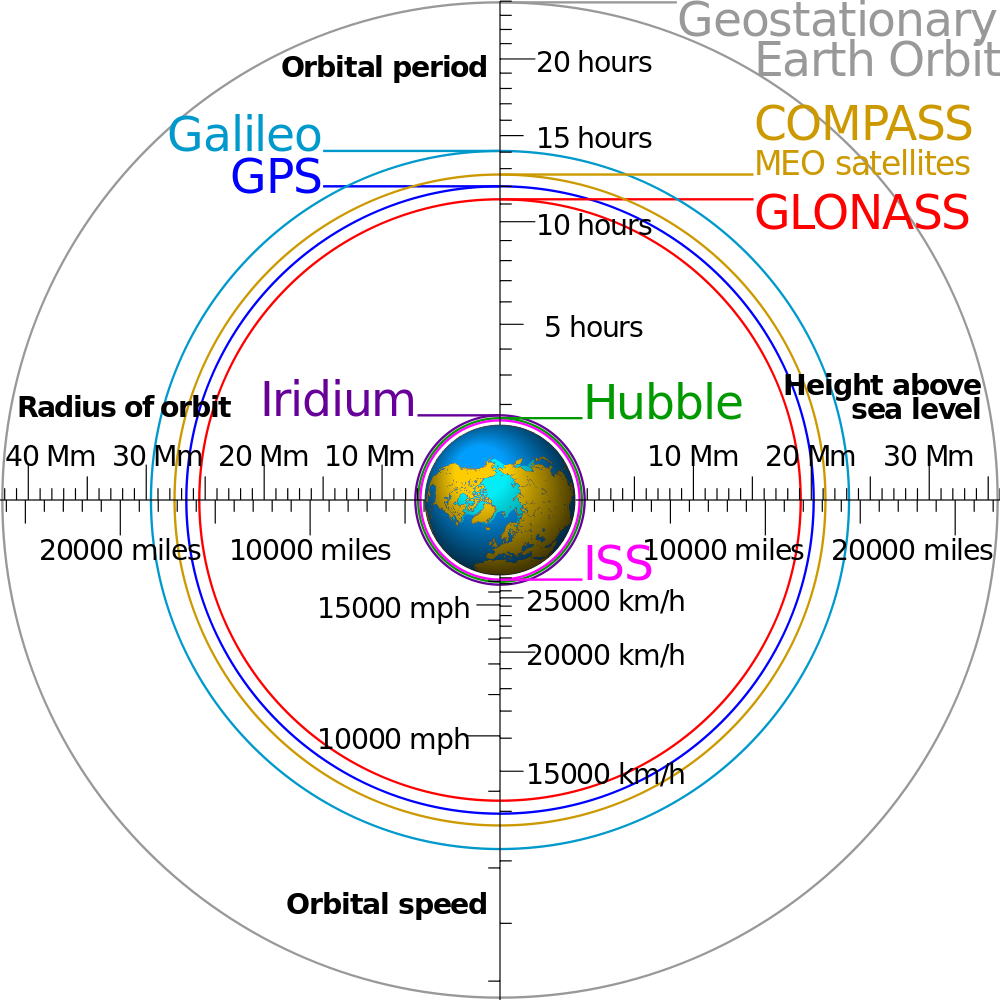
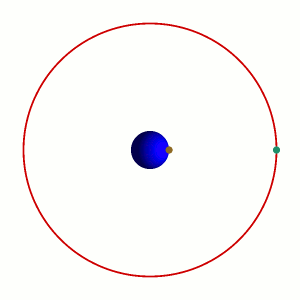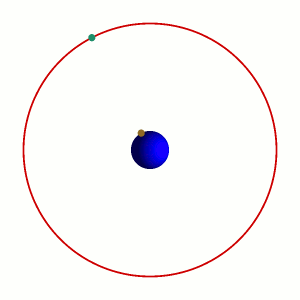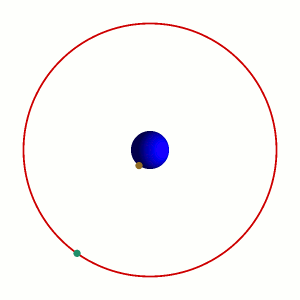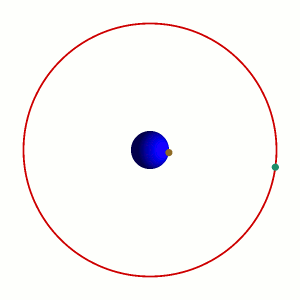
Aria Vuoto
→ Video su Youtube
 
"Pesa più un chilo di piombo o un chilo di paglia?"
In realtà il vecchio quesito è più sottile di quanto si crede.
Per comodità sostituiamo la paglia al polistirolo e poniamoci le seguenti domande:
  1. Se poniamo un kg di piombo o un kg di polistirolo su una bilancia,
    in quale dei due casi essa segnerà di più?
  2. Ponendo su una bilancia un blocco di piombo, essa segna esattamente 1 kg.
    Lo stesso vale se poniamo su di essa un blocco di polistirolo.
    Quale dei due blocchi ha la massa maggiore?
Moto circolare uniforme e oscillazione delle coordinate del punto ruotante
Moto descritto da

con il vettore r(t) collegante istante per istante l'origine con il puntino nero.
Gli altri due puntini rappresentano x(t) e y(t).
Come variano nel tempo i vettori velocità e accelerazione?
Li si immaginino
— applicati all'origine delle coordinate;
— al punto ruotante.
[→ v(t) e a(t) non hanno dimensioni spaziali e quindi, a rigore,
non andrebbero disegnati nel piano (x,y)! (anche se lo si fa... — idem per p(t) e F(t) )
Per questo motivo, nel problema 4 della lezione 4 veniva richiesto di disegnare i versori dei vari vettori.]
Moto circolare uniforme rappresentato nelle possibili variabili per descriverlo
 
Moto circolare uniforme animato (eseguendo lo script)
Moto circolare inizialmente uniforme e poi accelerato ('Animato' eseguendo lo script)
Script R: moto_circ_unif-accel.R → 'tradurre' in Python

Esperimento di Cavendish e 'misura della massa della Terra'

("L'uomo che pesò il mondo")
PDF su bayes.it (copia locale)
[Naturalmente c'è un 'piccolo' refuso di 'solo' 10-11 nell'ultima pagina in GCavendish]
 
A questo punto basta collegarlo all'uomo che misurò la Terra...

Eclisse parziale di Luna e Aristarco di Samo


Eclisse del 16 luglio 2019
→ provare a valutare il rapporto fra diametro delle Luna e quello della Terra
(ipotesi di "cilindro d'ombra" non perfetta, ma risultato più che ragionevole)
Massa all'interno di un guscio sferico (da Wiki)
[dimostrazione un po' tecnica — si può fare di meglio...]
ad libidum... (qui sembra ben fatta, praticamente simile a quanto abbiamo fatto noi)
Campo gravitazione (e accelerazione di caduta libera)
in funzione della distanza dal centro della Terra
(sul significato della linea verde tratteggiata torneremo nel seguito)
 
 
Nota: sulle ordinate viene riportata l'accelerazione di caduta libera, la quale vale -9.8 m/s2 per R=RT.
Tale variabile può essere anche reinterpretata come [Si noti inoltre la scala orizzontale in cui la distanza dal centro della Terra viene riportata in unità di raggi terrestri — i metri non darebbero la stessa percezione!]
Calcolo di volumi mediante integrali (*)
1. Cilindro (con r = R   ∀ x)
 
 
2. Cono (con r dipendente da x → trovare la relazione)
 
 
3. Sfera (con r dipendente da x → trovare la relazione)
(*) Note:
A proposito del principio di misura:
→ curiosa tazza con indicatore di livello
 
Funziona grazie a particolare materiale che da nero diventa rosso al di sopra di una certa temperatura:
Densimetro ad affondamento
Principio di misura: equilibrio fra forza peso e spinta di Archimede, la quale dipende dalla densità del liquido.
Spinta di Archimede + terzo principio della meccanica
           
 
[Archimede & Newton (3th Principle) at work]

Principio di funzionamento ('principio di misura') delle normali bilance: In questo caso, alla forza peso di bicchiere e acqua si aggiunge la reazione (diretta verso il basso) alla spinta di Archimede (diretta verso l'alto).
Nota: come visto a lezione con il tubetto di pastiglie, quello che conta
non è la massa dell'oggetto immerso, ma solo il suo volume:
→ principio utilizzato per 'misurare' il volume della maniglietta
"Cannone di Newton"
 

 
[ Dai Principia di Newton ]
   

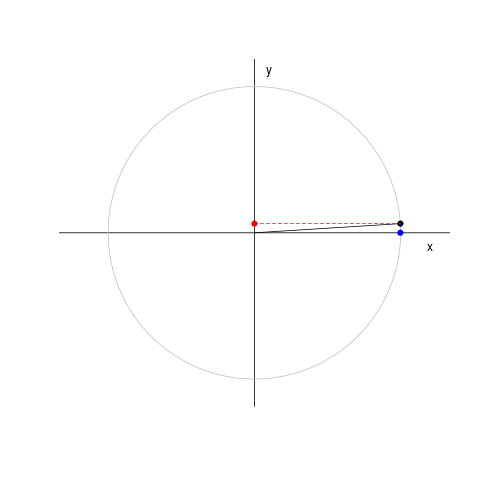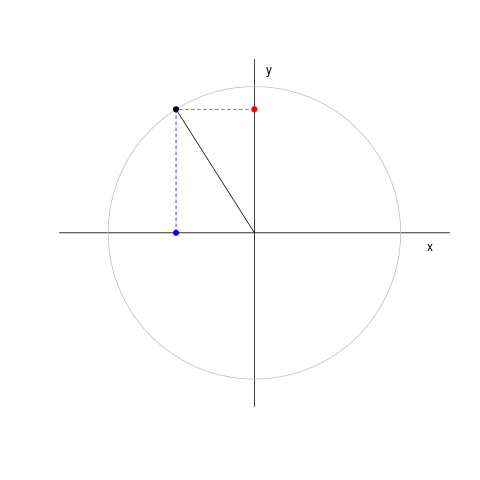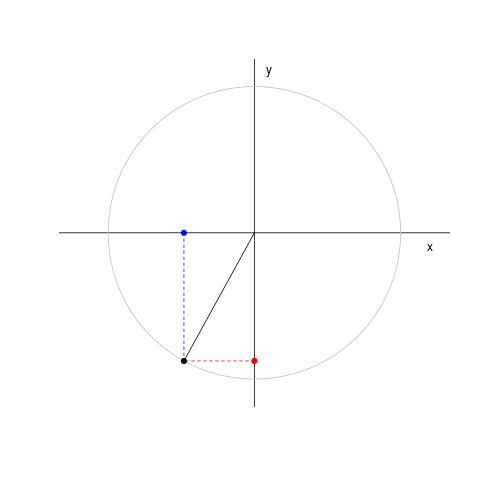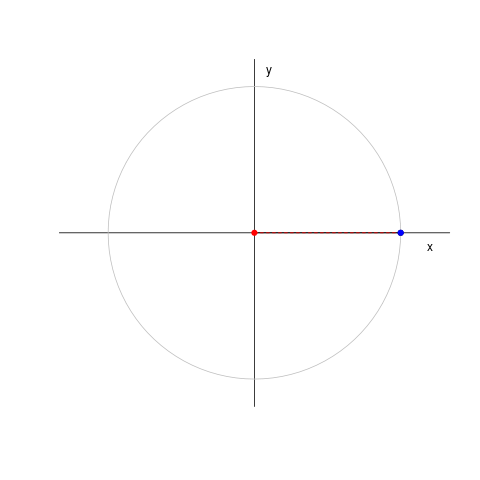
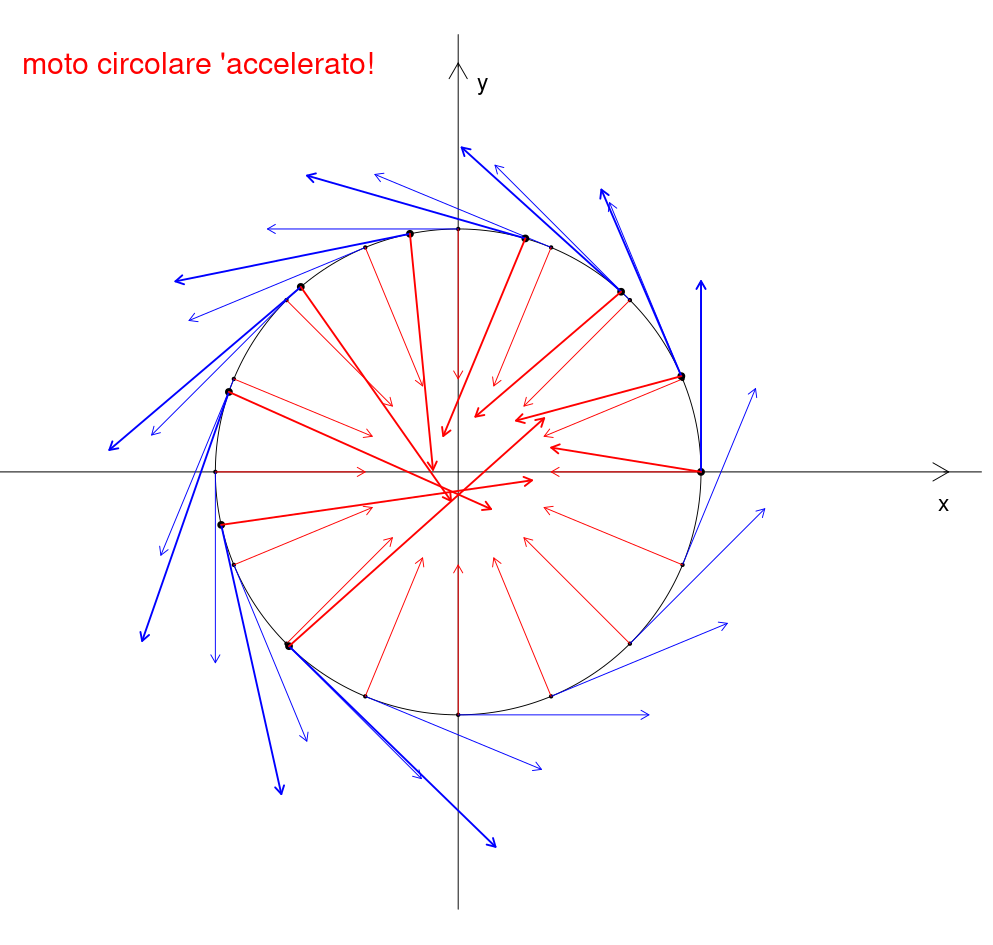
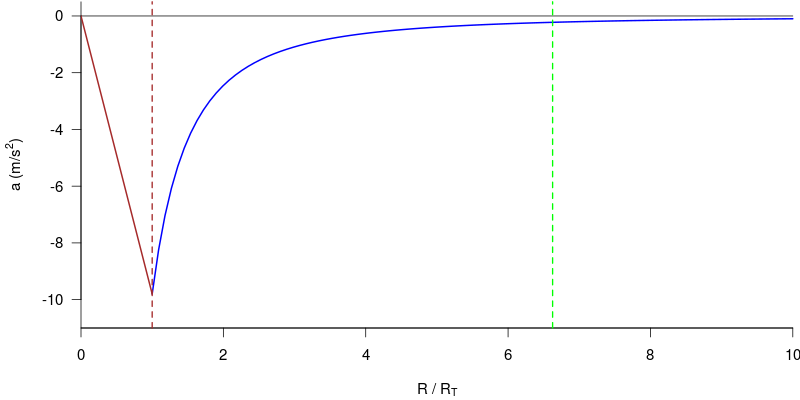
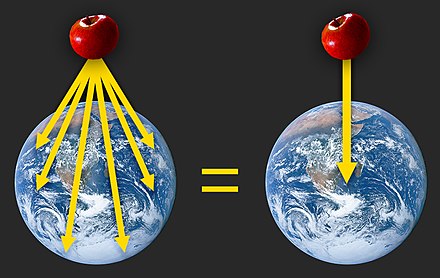
Il cosiddetto 'cannone di Newton' è un esperimento concettuale per far capire che le mele che cascano e la luna che gira derivano dalle stessi leggi della Fisica.

Accelerazione e velocità del 'sasso' lanciato verso l'alto
Semplice problema unidimensionale con → il resto è un semplice esercizio.
Azione e reazione... in azione
 
La sonda è spinta avanti dal gas espulso dietro:

 
 
  Il vapore espulso fa girare il recipiente:
 
 
  ... e la pista spinge l'atleta in avanti(*)
 
(*) ma non lo dite a chi non conosce il terzo principio, se no vi prendono per matti...
Azione e reazione in pratica
Chi vince, se le forze sono uguali e contrarie?
Attrazione fra un punto materiale di massa m e una sfera omogenea di massa M (da Wiki)
 
[In italiano: Teorema del guscio sferico]


[Animazione, per capire meglio l'integrale.]
 
La massa m è attratta da tutti i punti materiali all'interno della sfera di raggio R (e viceversa):
→ ne segue che la forza totale è la stessa che si avrebbe fra due punti materiali di massa M e m posti a distanza r.
(Dettagli del calcolo fuori programma)
 

Nota: la figura (da Wiki) potrebbe essere fuorviante
in quanto la lunghezza delle frecce indica la distanza fra mela e punto della Terra che l'attrae
e non l'intensità della forza, che notoriamente va come l'inverso del quadrato della distanza!
Da che distanza dalla base della Minerva è stata scattata questa foto?
(Misure di distanza effettuate mediante opportuna proporzione,
a proposito di principio di misura)
Dati Causa lavori in corso quest'anno questo problema non è in programma
 
"Il pollice di Fermi era il metro che aveva sempre a disposizione"
(da immaginarselo ventenne "in calzoni alla zuava e giacchetta alla tirolese"...)
da Atomi in Famiglia di Laura Fermi, p. 15.
Ancora misure di distanza 'per confronto'
 
Da che distanza dal Cupolone di San Pietro è stata effettuata, approssimativamente, questa foto? (Presa da flickr)
 

(Cliccare sopra per vedere l'intera foto — copia locale)
Note:

[ Vedi @dennisstever su Instagram, post del 28/11/2018 ]
 
Da che distanza è stata effettuata la foto? (ammesso che non sia un montaggio, ma la sostanza non cambia)
Diametri angolari (e dimensioni angolari)

 
 
 
[ Ma può essere più utile memorizzare i reciproci degli angoli espressi in radianti! ]
[ E, comunque, le dimensioni angolari variano da persona a persona ]
Eureka!
       
Vedi 'Eureka' su Wiki

Eratostene e la misura della circonferenza terrestre

(da http://www.artesolare.it/ — vedi anche su Rete di Eratostene)
 
Sulla storia della forma della Terra nella nostra cultura
si raccomanda una interessante conferenza di Alessandro Barbero
Esperimenti scioglimento ghiaccio
(Erica B.)
Lo strumento di calcolo a bordo dell'Apollo 13
Valutazione di π mediante estrazioni random ('Monte Carlo')
Codice R(*) [script file: pi_MC.R]
N=10000; x<-runif(N); y<-runif(N)
plot(x,y,col='cyan',asp=1)
sel <- x^2+y^2 <= 1
points(x[sel],y[sel],col='red')
4*sum(sel)/N
 
[(*) Installare R ed eseguire i comandi; 'tradurre' in Python; provare a variare N]
Integrale mediante estrazioni random ('Monte Carlo')
Funzione: sin^2(x)
limiti: da 0 a π
Codice R(*) [script file: int_sin2_MC.R]
N=10000; x<-runif(N,0,pi); y<-runif(N)
plot(x,y,col='cyan')
sel <- y <= sin(x)^2
points(x[sel],y[sel],col='red')
sum(sel)/N * (1*pi)
 
[(*) Installare R ed eseguire i comandi; 'tradurre' in Python; provare a variare N]
 
↠ Integrale esatto ottenuto mediante Wolfram Alpha
↠ Antiderivata di interesse
Integrale numerico
Funzione: sin^2(x)
limiti: da 0 a π
[numero di intervalli volutamente piccolo (per capire meglio)]
Script R: int_sin2_num.R
↠ eseguire lo script R; 'tradurlo' in Python (anche senza la parte grafica); provare a variare N