- Definizioni del metro dal 1791 ai giorni nostri (frazione del meridiano; barra platino-iridio; lunghezza d'onda di particolare radiazione elettromagnetica; spazio percorso dalla luce in una frazione di secondo).
- Dalle unità di misura antropomorfe alle unità di misura prese dalla natura.
- Particolari esigenze metrologiche nella Francia del XVIII secolo, ruolo culturale (Illuminismo) e pratico della rivoluzione.
- Meridiano o equatore? Escursus su misura di archi terrestri e
dei metodi per misurare latitudine e longitudine.
Forma della Terra: sfera -> ellissoide -> geoide. - Perché il quarto di meridiano e non la sua metà o la sua interezza, ovvero perché non raggio o diametro?
- Cosa si misura in pratica e cosa si estrapola. Impossibilità di misura diretta polo-equatore e fattibilità della misura nella sola Francia. Importanza dello schiacciamento della Terra. Spedizioni per la misura di archi di meridiano e spedizione 1792-1798 per misurare 'il "meridiano di Parigi" da Dunquerque a Barcellona.
- Problemi politici legati a tale scelta dell'unità di misura e crisi della collaborazione internazionale.
- "Non si poteva scegliere qualcosa meno complicato?"
-> correlare l'unità di misura del tempo (a quei
tempi basata sul giorno, diviso in 24 ore, etc)
a quella della lunghezza
- Inizialmente: pendolo
- Ora: velocità della luce
- Richiamo delle proprietà del pendolo
- Il pendolo del secondo
- Tito Livio Burattini, il metro cattolico e il peso cattolico.
- Il pendolo: piombo da pesca sportiva da 300 g forato;
lenza; filo di scoubidou per ridurre le oscillazioni del
filo dentro il foro; vite di blocco.
(Piccola discussione su importanza di alta densità: il lavoro compiuto dalla resistenza dell'aria ad ogni oscillazione va come la sezione, ovvero come R2, mentre l'energia meccanica iniziale va come la massa, ovvero come ρR3.) - Punto di sospensione: architrave della porta (rappresenta uno dei punti più delicati del'esperimento e sicuramente il più debole della nostra realizzazione).
- Misure: 10 periodi a testa; inizialmente studio in funzione dell'angolo di oscillazione, successivamente solo 'piccole' oscillazioni al variare lunghezza.
- Prime osservazioni sui dati: effettivamente si nota dipendenza del periodo dall'ampiezza; il 'metro cattolico' sembra essere lungo un metro (c.a 99cm): strana coincidenza, date le due definizioni assolutamente scorrelate.
- Lavoro (per cominciare):
- studio empirico del periodo del pendolo in funzione della sua lunghezza: che legge segue? Riportare punti su carta millimetrata lineare e logaritmica.
- studio empirico del periodo del pendolo in funzione dell'angolo di oscillazione: che legge segue?
- Determinazione della lunghezza del 'pendolo del secondo' (semiperiodo!) mediante interpolazione grafica, usando 1) interpolazione lineare; 2) l'andamento che meglio riproduce l'andamento empirico.
- P. Agnoli e G. D'Agostini, Perché il metro batte il secondo? (per dettagli vedi articolo in inglese ivi citato e distribuito durante l'incontro).
- P. Agnoli, Da cosa origina il metro? (rubrica "Chiedi all'esperto!" di Scienza per tutti dei Laboratori Nazionali di Frascati).
- D. Sobel, Longitudine, Rizzoli.
- D. Guedj, Il metro del mondo, Longanesi.
- K. Alder, La misura di tutte le cose, Rizzoli.
- Nell'Isola misteriosa di Giulio Verne viene descritto bene come misurare latitudine e longitudine e l'importanza.
- Infine, il problema della longitudine è anche trattato nell'Isola del giorno dopo di Umberto Eco.
- In letteratura, inclusi manuali ed enciclopedie,
c'è abbastanza confusione sull'esatta definizione
originaria del metro:
- Non era "1/40.000.000 dell'equatore terrestre" [Ma pià avanti nello stesso link, è riportata la definizione corretta, anche se non è vero che era definito sul Meridiano di Parigi, ma su un qualsiasi meridiano.]
- Questo secondo errore (Meridiano di Parigi nella definizione)
si trova anche sull'Encarta, versione inglese, ove viene anche detto
che "Later, after it was discovered that the Earth is not
a perfect sphere, the standard meter was defined as the distance
between two fine lines marked on a bar of platinum-iridium alloy"
[in realtà, che la Terra non fosse sferica era già ben noto,
ma si pensava fosse ma ellissoide; il problema è che essa
ha una figura ben più complicata ('geoide') che non
corrisponde a nessun solido di rotazione.]
Nella versione italiana (vedi Encarta 2002) la cosa diventa addirittura comica, in quanto si riporta che "le difficoltà ad applicare tale definizione, causate dalla forma sferica della terra"(!!).
- Un (apparententemente) banale esercizio di cinematica:
- una certa distanza è percorsa nella prima metà
con velocità
v1 e la seconda con
velocità v2: trovare
velocità media sull'intero percorso.
- => non è la media aritmetica delle velocità! (bensì la media armonica);
- => diverso il caso in cui si viaggia per metà tempo a v1 e metà tempo a v2 (-> media aritmetica delle velocità)
- una certa distanza è percorsa nella prima metà
con velocità
v1 e la seconda con
velocità v2: trovare
velocità media sull'intero percorso.
- Leggi della meccanica ("i tre principi di Newton")
- Moto di un corpo soggetto a forze:
- forza nulla -> accelerazione nulla -> velocità costante;
- forza costante -> accelerazione costante -> moto uniformemente
accelerato
- rappresentazione grafica;
- formule del moto uniformemente accelerato
- forza variabile (in principio dipendente da posizione, velocità e tempo): ??
- Analisi su intervalli di tempo molto piccoli, applicando a ciascuno di
essi le formule del moto uniformemente accelerato
soluzione numerica (in contrapposizione
a soluzione analitica, ovvero mediante integrali,
che sono fuori programma).
-> Vedi esempi sul sito del corso di Fisica 1 per informatici, in particolare- Problema della gittata, incluso calcolo dello spazio percorso lungo la traiettoria e anche tenendo conto di resistenza dell'aria: gittata.r (in R);
- Moto lungo la verticale in presenza di gravità, con soluzione sia esatta che approssimata ('integrale numerico') lancio.c (in C);
- Soluzione numerica dell'oscillatore armonico: oscillatore_gp.c (in C),
- Pendolo: soluzione numerica, con o senza approssimazione per piccoli angoli pendolo.c (in C).
- Foglio di calcolo oscillatore.sxc (OpenOffice.org)
- Foglio di calcolo oscillatore.xls (MS Excel)
- Spiegazioni (significato delle varie colonne)
- Analisi su intervalli di tempo molto piccoli, applicando a ciascuno di
essi le formule del moto uniformemente accelerato
soluzione numerica (in contrapposizione
a soluzione analitica, ovvero mediante integrali,
che sono fuori programma).
- Analisi di velocità, accelerazione e forza di oggetto lanciato per aria verticalmente.
- Bilancio delle forze: caso di oggetto posato su un piano, tirato da un elastico ('dinamometro') ma fermo a causa della forza di attrito
- Inventario delle coppie azione-reazione
- Molla disposta verticalmente alla quale vengolo aggiunti pesetti: bilancio
delle forze all'equilibrio.
- Misure in aula
- allungamento in funzione della massa applicata;
- periodo di oscillazione in funzione della massa applicata.
- Relazione fra forza e spostamento (orientato) x dalla posizione 'equilibrio: F = -k x
- Relazione fra accelerazione e spostamento x dalla posizione 'equilibrio: a = -(k/m) x
- Dimensioni di k/m, di sqrt(k/m) e del suo reciproco: (-> tempo caratteristico)
- Misure in aula
- Problema del pozzo per il centro della Terra
- Relazione fra forza e posizione (orientata) r dal centro della Terra: F = - K r (K &egarve; altra costante);
- Relazione fra accelerazione e spostamento r dalla posizione 'equilibrio: a = -(K/m) r = -(g/RT) r
- Dimensioni di g/RT, di sqrt(g/RT) e del suo reciproco: (-> tempo caratteristico)
- Analisi del pendolo
- Decomposizione della forza peso.
- Richiami di ('introduzione a') trigonometria mediante triangoli rettangoli simili, con applicazione a misura di latitudine ed elementi di triangolazione per misurare altezza di lampioni e palazzi.
- Relazione fra forza tangente e angolo (orientato) α rispetto alla posizione di equilibrio: F = -m g sin(α);
- Relazione fra accelerazione e angolo (orientato) α rispetto alla posizione di equilibrio: a = - g sin(α);
- Relazione fra accelerazione angolare e angolo (orientato) α rispetto alla posizione di equilibrio: aα = - (g/l) sin(α);
- Approssimazione per piccoli angoli ('α < 0.1', ovvero circa 5-6 gradi.) aα = - (g/l) α;
- >Dimensioni di g/l, di sqrt(g/l) e del suo reciproco: (-> tempo caratteristico)
- Analogie fra i tre problemi:
- Sempre del tipo
accelerazione = - (costante positiva) × (spostamento da posizione di equilibrio) - con 'costante positiva' che ha le dimensioni
t -2 e che chiamiamo
ω2
-> il reciproco della radice quadrata della costante rappresenta un tempo caratteristico del fenomeno, che per ora indichiamo con tc. - Cosa rappresenta tc? Usiamo le misure fatte con la molla per confrontare empiricamente tc con un altro tempo caratteristico del fenomeno, il periodo T misurato per vari valori di m.
- Sempre del tipo
- Circonferenza di raggio R percorsa con velocità
v, costante in modulo (ma ovviamente di direzione e verso variabile):
- Periodo (tempo per fare un giro, ovvero di percorrere 2πR): T = 2πR / v;
- Velocità angolare:
angolo percorso per unità di tempo,
ove gli angoli sono misurate nella loro 'unitaà naturale'
il radiante. Un giro corrisponde a 2π radianti ed è
effettuato, per definizione, in un periodo T. Quindi
la velocità angolare, indicata usualmente con ω,
vale 2π/T. Inoltre, essendo
T = 2πR / v, essa può essere anche scritta come
2π / (2πR / v) = v/R, da cui, riassumendo:
ω = 2π/T = v/R
v = ωR
T = = 2πR = 2π/ω - Frequenza, numero di giri nell'unità di tempo.
Siccome ogni giro si effettuano 2π radianti,
il numero di giri al secondo è pari alla velocità
angolare diviso 2π, ovvero f = ω/2π = 1/T.
[Il simbolo per la frequenza è anche la lettera greca ν, 'nu' (che per motivi misteriosi, negli ultimi decenni nei licei viene pronunciata 'ni'...), che però sul browser si confonde la la 'vu', per questo qui usiamo f.] - Accelerazione centripeta: dimostrazione geometrica mediante variazione del vettore velocità e dell'uso di triangoli simili: Δr/r = Δv/v -> Δv = (Δr/r) v -> a = Δv/Δt = v2/r -> ac = v2/R.
- Forza centripeta: massa × accelerazione centripeta: Fc = m v2/R.
- Accelerazione delle prioezioni sugli assi coordinati.
Essendo l'accelerazione centripeta sempre diretta verso il centro
del cerchio, essa è di verso opposto
al raggio vettore, ovvero
ac = - ω2r,
le sue proiezioni sono nella stessa relazione con le coordinate
x e y:
ax = - ω2x
ay = - ω2y
[Questi ultimi punti saranno ripresi al prossimo incontro]
- Satellite in orbita radente alla superficie terrestre:
- Moto circolare uniforme con velocità v incognita e raggio RT -> forza centripeta pari a m v2/RT.
- La forza centripeta è dovuta alla
forza di gravità, ovvero
m v2/RT = G MT m / RT2.
['È dovuta' sta ad indicare che la forza è una sola, quella di gravità che, in questo caso, ha il ruolo di forza centripeta.] - Semplificando m [massa inerziale = massa gravitazionale!],
e risolvendo per v, otteniamo:
v = sqrt(g RT)
T = 2π sqrt(RT/g)
ω = sqrt(g/RT).- Siccome conosciamo la relazione che intercorre fra accelerazione delle proiezioni e proiezioni stesse, scegliando l'asse x lungo il pozzo per il centro della Terra del problema precedente, otteniamo
= - (g/RT) x. Ovvero, con la notazione usata nel problema del pozzo: ar = - ω2r = - (g/RT) r.
ax = - ω2x - Siccome conosciamo la relazione che intercorre fra accelerazione delle proiezioni e proiezioni stesse, scegliando l'asse x lungo il pozzo per il centro della Terra del problema precedente, otteniamo
- Il movimento del sasso nel pozzo per il centro della terra è
esattamente uguale alla proiezione (lungo il diametro)
di un moto circolare uniforme di un satellite in orbita radente
intorno alla Terra: -> moto oscillatorio
(-> oscillatore armonico):
r = RT cos ωt,
avendo scelto per t=0 l'istante in cui il sasso viene fatto cadere del pozzo 'dalla nostra parte', ovvero r(t=0) = +RT .
- Il moto di un corpo in un pozzo (ideale) per il centro della Terra è pari a quello della proiezione lungo il pozzo di un corpo in orbita (ideale) in orbita radente alla superficie terrestre.
- Ogni qual volta abbiamo una relazione fra accelerazione e
generica coordinata z del tipo
az = - (costante positiva) z
il moto lungo la coordinata z può essere visto come la proiezione di un ipotetico moto circolare uniforme che si svolge con velocità angolare pari alla radice quadrata della costante positiva che compare nell'equazione. - Possiamo scrivere quindi, in generale
az = - ω2 z
e una volta che conosciamo ω in funzione dei parametri fisici del problema, ci possiamo ricavare il periodo. - Riassumendo, abbiamo, per i tre problemi che ci interessano:
Problema ω2 ω T Molla k/m sqrt(k/m) 2π sqrt(m/k) Pozzo centro Terra g/RT sqrt(g/RT) 2π sqrt(RT/g) Pendolo g/l sqrt(g/l) 2π sqrt(l/g) - Si noti come soltanto nel caso del problema del pozzo esiste un'altro problema fisico che ha come soluzione un moto circolare uniforme e di cui il problema in esame è effettivamante la proiezione. Negli altri due casi tale moto circolare è puramente immaginario. In particolare, nel caso del moto del pendolo, non va assolutamente confuso l'angolo di oscillazione del pendolo con l'angolo dell'ipotetico moto circolare uniforme associato!
- Ogni problema fisico che si riconduce ad una relazione fra 'accelerazione' e 'posizione' del tipo az = - ω2 z viene denominato oscillatore armonico, anche nei casi in cui per 'posizione' si intende una generica variabile (ad esempio la carica in un condensatore) e per 'accelerazione' la variazione nel tempo della variazione nel tempo della variabile (ad esempio la variazione nel tempo della corrente elettrica che entra nel condensatore).
- A proposito, si noti inoltre, come ω ha il significato
di velocità angolare; solo nel caso del moto circolare
uniforme. Nel caso di oscillatore armonico, la grandezza indicata
con lo stesso simbolo e legata al periodo dalla stessa relazione
(ω T = 2π) si chiama pulsazione.
- Dettagli equazioni molla e pozzo per il centro della Terra: file ps e pdf
- Per le questioni di Fisica Generale, si consulti il proprio manuale di Fisica, integrato con gli appunti delle lezioni.
- Chi è personalmente interessato all'uso del linguaggio R (fuori programma) può vedere qui.
- L'equazione oraria della variabile descritta da oscillatore armonico
è, in generale, del tipo
z(t) = Z0 cos(ωt + φ),
la quale si riduce a
z(t) = Z0 cos(ωt)
se scegliamo opportunamente t, ove Z0 sta, in generale, per scostamento iniziale dalla posizione di equilibrio. - L'espressione dell'accelerazione nel tempo si ottiene ricordando la
relazione generale az = - ω2 z:
az(t) = - &omega2 Z0 cos(ωt). - Per quanto riguarda la velocità vz, ci dobbiamo
ricordare che essa è la proiezione della velocità
dell'ipotetico moto circolare uniforme. La possiamo valutare
in due modi:
- Il vettore velocità, di modulo
ωR, è sempre normale al raggio vettore
ed è quindi anch'esso un vettore ruotante, che però
anticipa di 90 gradi (π/2) il raggio vettore. Quindi la
ciascuna proiezione del vettore velocità anticipa di
90 gradi la rispettiva proiezione del raggio vettore:
v(t) = ωR cos(ωt + π/2) = - ωR sin(ωt).
Per la generica variabile z diventa quindi
vz(t) = - ωZ0 sin(ωt). - [Sempre ragionando sul vettore ruotante velocità in un moto
circolare uniforme, considerando la proiezione lungo l'asse x
e con t=0 quando la particella è in x=R:
- essendo il modulo pari a ωR e dovendo avere un'oscillazione, l'espressione deve contenere ωR per il seno o coseno di ω;
- essendo la proiezione inizialmente nulla la 'funzione giusta' è il seno;
- essendo inoltre la velocità inizialmente negativa (la coordinata x, essendo inizialmente al suo massimo, non può che diminuire), ci deve essere anche un segno meno
v(t) = - ωR sin(ωt).
e per la generica z
vz(t) = - ωZ0 sin(ωt)] - Per quanto riguarda l'accelerazione, il vettore accelerazione
ruota anch'esso con velocità angolare ω,
ha modulo &omega2R ed, essendo ortogonale
al vettore velocità e 'antiparallelo' al raggio vettore,
&egarve; in anticipo di 90o sul vettore velocità
e di 180o sul raggio vettore. Quindi:
a(t) = ω2R cos(ωt + π) = - ω2R cos(ωt).
Per la generica variabile z diventa quindi
az(t) = - ω2Z0 cos(ωt).
- Il vettore velocità, di modulo
ωR, è sempre normale al raggio vettore
ed è quindi anch'esso un vettore ruotante, che però
anticipa di 90 gradi (π/2) il raggio vettore. Quindi la
ciascuna proiezione del vettore velocità anticipa di
90 gradi la rispettiva proiezione del raggio vettore:
- Ricapitolando
- Moto armonico <---->
az =
- ω2 z :
T = 2π/ω z(t) = Z0 cos(ωt vz(t) = - ωZ0 sin(ωt) az(t) = - &omega2 Z0 cos(ωt)
- Moto armonico <---->
az =
- ω2 z :
- Esperimento dello scopettone.
- Misura del coefficiente di attrito statico mediante l'esperimento del piano inclinato.
- Semplici misure (vedi capitolo 2 dispensa distribuita). In particolare
- Errore di lettura e di cronometraggio: leggende metropolitane e verifica sperimentale.
- Documentazione del lavoro di laboratorio (cap.3): logbook, relazione etc..
In particolare:
- cifre significative: significato e propagazione ('cum grano salis').
- Analisi grafiche e linearizzazioni(cap.6).
In particolare
- carte logaritmiche ('semilogaritmiche' e 'doppiologaritmiche').
- GdA, Le basi del metodo sperimentale, Parte 1, vedi qui.
- Logaritmi: vedi in questo sito, o qui per saperne di più (soprattutto sulla funzione logaritmo!).
Esperimento di termalizzazione -> andamento esponenziale -> linearizzazione su carta semilog.
- Realizzazione dell'esperimento: termometro estratto da acqua calda e posto su tavolo:
misure di temperatura in funzione del tempo.
[Variazioni sul tema: raffreddamaneto della stessa quantità di acqua in diversi recipienti di vetro o plastica di uguale spessore delle pareti (per studiare cosa cambia variando il rapporto fra volume e area), con diversi spessori o aggiungendo materiali coibententi).]
- Visualizzazione dei dati in carta lineare e carta semilog.
- Determinazione grafica della costante di tempo τ dell'andamento logaritmico: da fare
nella relazione
(vedi lezione precedente per dettagli).
Nota: Il risultato sperimentale mostra un andamento non perfettamente esponenziale negativo (ovvero non perfettamente lineare su carta semilog). A parte errori strumentali, sembra che ci siano due andamenti esponenziali sovrapposti: uno a piccoli tempi, probabilmente dovuto al raffreddamento iniziale della colonnina di mercurio a contatto con l'aria; successivamente la velocità di raffreddamento diminuisce in quanto il legno della base del termometro fornisce calore lentamente al mercurio. (Si ricorda che i termometri buoni si erano rotti durante il trasporto e sono stati acquistati due termometri da parete nella prima ferramenta incontrata!).
->Non ha molto senso tracciare una sola retta su tutti i punti (su grafico semilog). Si raccomanda quindi di tracciare due rette:- la prima fino a 15 secondi;
- la seconda da 20 secondi in poi.
- Morale: nella fisica sperimentale non tutti i guai vengono per nuocere, in quanto permettono di imparare (ovviamente non abbiamo avuto tempo per cambiare strumentazione e capire se veramente l'effetto osservato è dovuto alla causa ipotizzata).
Origine degli andamenti esponenziali (e motivo dell'importanza e della naturalezza della costante e di Eulero e, di riflesso, dei logaritmi naturali).
Alcuni problemi apparentemente molto diversi fra di loro:
- Termalizzazione: il calore scambiato nell'unità di tempo è proporzionale
alla differenza di temperatura, con un coefficiente che dipende dalle proprietà
fisiche e geometriche della superficie di contatto.
Chiamando t il tempo, T la temperatura istantanea del corpo, TA la temperatura ambiente, θ la differenza fra T e TA, Q la quantità di calore, C la capacità termica (legata al calore specifico c dalla relazione C = c m, ove m è la massa del corpo) e η un coefficiente da cui dipende la dispersione termica, abbiamo:
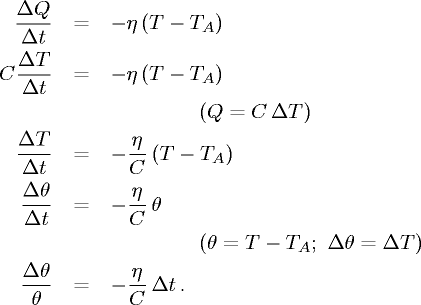
- Corpo frenato da attrito di viscosità proporzionale alla velocità
con coefficiente di proporzionalità β. Con i soliti simboli per
forza, massa e velocità otteniamo:
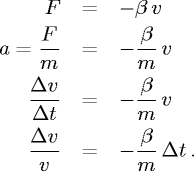
- Scarica di un condensatore di capacità C su una resistenza R.
Indicando, inoltre con I la corrente elettrica, di verso scelto tale che
una corrente positiva riduce la carica del condensatore, abbiamo:
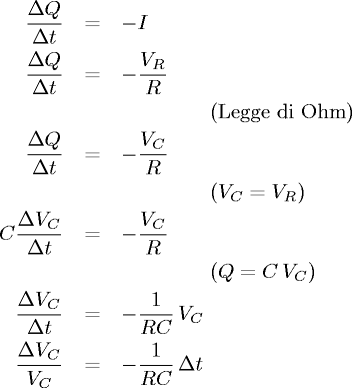
- Aumento/decremento di popolazione (assumento tasso di crescita/decrescita costante):
l'incremento di popolazione n nell'unità di tempo è
proporzionale al numero
di individui della popolazione e da una costante. Chiamiamo &alpha
il coefficiente di proporzionalità, (positivo se le nascite supera il numero
di morti e negativo nel caso contrario; nullo nel caso di 'crescita zero'),
otteniamo:
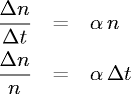
- Aumento di capitale, dato un tasso di interesse i nel tempo unitario: -> analogo a crescita di popolazione, con α solo positivo.
- Decadimento di nuclei radioattivi: -> analogo
a crescita di popolazione, con α solo negativo.
.
-> la variazione relativa ('percentuale') della variabile è proporzionale all'intervallo di tempo.
Possiamo riscrivere la stessa equazione come
-> il tasso di crescita/decrescita (a seconda del segno di α) di una variabile è proporzionale al valore della variabile.
Si tratta ora di capire come varia x con il tempo. Cominciamo a vedere cosa succede dopo Δt, dopo 2Δt, etc., partendo dal valore x0 all'istante t=0:
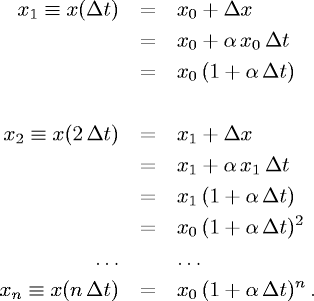
Si tratta quindi di una progressione geometrica di ragione (1+αΔt), maggiore o minore di 1 a seconda del segno di α.
Dopo un tempo t = nΔt si ha quindi

Immaginiamo di 'affettare' ora il tempo t in tantissimi intervallini Δt. Al limite, il numero di intervallini diventa infinito e la loro ampiezza nulla.. Si tratta di trovare quindi il limite

Cerchiamo di capire quanto vale questo limite in modo 'pratico', non rigoroso, analizzando la seguente tabella compilata con αt=1 e αt=-1.
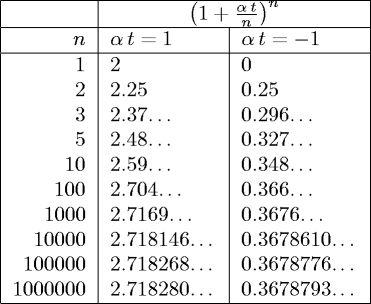
Come si può verificare facilmente, il limite converge a eαt, ove e è la costante di Eulero, base dei logaritmi naturali (in effetti, vedi bibliografie, una delle definizioni di e è proprio legata a questo limite.
In conclusione, la soluzione cercata è
Finalmente, sostituendo ad α i parametri dei diversi problemi, abbiamo le diverse soluzioni:
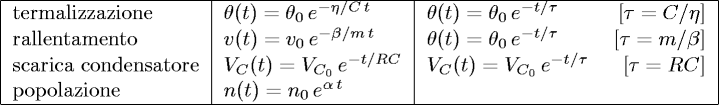
Nella tabella abbiamo indicato, ove ha interesse, con τ la costante di tempo del processo, un parametro che ci indica, in qualche modo, la velocità del processo: minore è τ, più rapido è il processo. In particolare, si noti come, nel caso di esponenziali negativi (i primi tre casi), per t=τ la grandezza in esame di riduce di 1/e rispetto al valore iniziale, ovvero di circa il 37% (si ricorda come θ rappresenta la differenza di temperatura rispetto all'ambiente).
Nel caso della termalizzazione e del rallentamento si cerchi di dare una giustificazione intuitiva delle dipendenze delle costanti di tempo dai parametri del problema.
Altro esempio didatticamente interessante di crescita esponenziale: il tacchino esponenziale (suggerito dal Prof Barra): mangia proporzionalmente al suo peso e aumento di peso esattamente di quanto mangia.
Bibliografia
- Costante e di Eulero: vedi qui o qui (quest'ultimo soprattutto per l'equivalenza fra le due definizioni più note).
| Iniziali | 1 | 2 | 3 | 4 | tot | % |
| M.A. | 4 | 5 | 5 | 2 1/3 | 16 1/3 | 81.7 |
| F.D. | 0 | 3 | 0 | 2 1/3 | 5 1/3 | 26.7 |
| G.F. | 4 | 4 | 4 | 2 | 14 | 70.0 |
| C.M. | 4 | 4 | 4 | 3 1/3 | 15 2/3 | 78.3 |
| A.P. | 4 | 5 | 4 | 5 | 18 | 90.0 |
| C.S. | 4 | 5 | 5 | 3 2/3 | 17 2/3 | 88.3 |
| A.S. | 0 | 3 | 2 1/3 | 2 1/3 | 7 2/3 | 38.3 |
| M.S. | 4 | 5 | 5 | 5 | 19 | 95.0 |
- Quesiti
riguardanti gli argomenti delle prime tre lezioni. La prova,
della durata di 60 minuti si terrà all'inizio
dell'incontro del 22 aprile.
Programma:- Origine e definizione moderna del metro. Il metro cattolico di Burattini. Misure di latitudine e longitudine.
- Cinematica: velocità e accelerazione; moto rettilineo (o curvilineo) uniforme e moto uniformemente accelerato; moto circolare uniforme (inclusi angoli in radianti, velocità angolare e accelerazione centripeta): formule che legano le varie grandezze (R, α, v, ω, T, f e a).
- Principi della meccanica (leggi di Newton), loro significato ed uso in problemi elementari. Alcuni esempi di forze: forza di gravità (espressione sia in prossimità della superficie terrestre che in generale: -mg e -GMm/r2); forza della molla; forza di attrito statico e dinamico; reazioni vincolari. Composizione delle forze. Significato della forza centripeta (è semplicemente il nome che si dà ad una generiza forza se essa tiene un corpo su una traiettoria circolare!).
- Esempi studiati in dettaglio: molla, pozzo per il centro della Terra, pendolo e satellite in orbita radente intorno alla Terra.
- Oscillatore armonico e sua relazione con moto circolare uniforme: posizione, velocità ed accelerazione in funzione del tempo.
- Elementi di trigonometria: significato geometrico
di seno, coseno e tangente; funzioni sin(), cos() e tan()
e loro inverse asin(), acos() e atan().
(Nota: niente formule trigonometrice complicate; solo quello che ci serve per i problemi incontrati.) - Logaritmi: definizione e proprietà.
Logaritmo in base 10 [log10()]
e in base e, o naturali [log() o ln()].
Logarirmi e loro funzioni inverse. In particolare
esponenziale [ex o
exp(x)].
Uso di scale e carte logaritmiche ('semilog' e 'doppiolog').
Dettaglio risultati.Quesito M.A. F.D. G.F. C.M. A.P. C.S. A.S. M.S. 1 5 - - 5 7 3 - 8 2 3 - 3 0 3 3 - 10 3 10 3 0 0 - 8 - 7 4 10 10 0 - - 10 - - 5 8 - 2 10 - 10 - 8 6 10 - 0 - - - - 6 7 - - 0 0 - - 10 8 8 5 - 0 - - 2 0 0 9 10 8 0 8 0 0 7 8 10 10 - - 0 - 0 - 0 11 8 - - 4 - 0 - 8 12 - - 10 - 10 10 10 7 13 - - - - 0 0 0 - 14 8 - - - 0 - - - 15 0 0 - - 3 3 0 - 16 10 10 10 - 0 - 10 10 17 - - 4 - 0 - 8 - 18 - - 3 4 4 - 6 6 19 10 - 5 0 10 - 5 10 20 5 5 10 0 10 - 10 0 21 10 - - - - - 10 3 22 0 - 5 10 - - - 2 23 10 10 - 10 10 10 10 10 24 10 10 - 10 5 - 5 10 25 - - - - - - - - 26 - - - - - - - - 27 - - - - - - - - 28 - - - - - - - - voto
(decimi)5.1 2.0 1.9 2.2 2.2 2.1 3.3 4.3 - Relazione su esperimenti svolti in aula.
Consegna entro mercoledi 3 maggio.
| Valutazione | M.A. | F.D. | G.F. | C.M. | A.P. | C.S. | A.S. | M.S. |
| Partecipazione | 8.2 | 2.7 | 7.0 | 7.8 | 9.0 | 8.8 | 3.8 | 9.5 |
| Prova scritta | 5.1 | 2.0 | 1.9 | 2.2 | 2.2 | 2.1 | 3.3 | 4.3 |
| Relazione | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 7.5 |
| Totale (trentesimi) |
17 | 9 | 13 | 14 | 15 | 15 | 11 | 21 |