Dettaglio degli argomenti trattati a lezione

template di questi appunti, con info su html

Nota: si prevede che questi appunti saranno più stringati di quelli dello scorso anno.
Si fa quindi riferimenti ad essi per dettagli, approfondimenti e link.

[]

Nr.	Giorno		Nr.	Giorno		Nr.	Giorno
0	preliminari		8	Lunedì 15/11		16	Giovedì 16/12
1	Mercoledì 20/10		9	Giovedì 18/11		17	Lunedì 10/1
2	Giovedì 21/10		10	Lunedì 22/11		18	Giovedì 18/1
3	Lunedì 25/10		11	Giovedì 25/11		19	Giovedì 20/1
4	Giovedì 28/10		12	Lunedì 29/11		20	Lunedì 25/1
5	Giovedì 4/11		13	Giovedì 2/12		21
6	Lunedì 8/11		14	Giovedì 9/12		22
7	Giovedì 11/11		15	Lunedì 13/12		23

Raccomandazioni preliminari (prima dell'inizio)

• Sia perché non rimaniate troppo inattivi sia per cominciarvi ad familiarizzare con lo stile del corso molto interattivo (chi ha in programma di venire a seguire passivamente le lezioni, pensando di cominciare a studiare verso Natale o dopo, fa meglio a cambiare subito piano di studi), propongo una serie di attività, di cui 'render conto' (niente voti ma mi aspetto che ciascuno possa partecipare attivamente a discussioni su tali argomenti) nelle primissime lezioni:
  • Attività di ripasso (soprattutto per i matematici, ma anche i fisici stiano attenti a non 'presumere' troppo):
    • Questioni di base di cinematica e meccanica, soprattutto cercando dei modi per spiegare tali cose in modo semplice ai futuri allievi (velocità, accelerazione, forze, moto circolare, pendolo, molla, attrito);
    • gravità e leggi di Keplero;
    • moti planetari nell'approssimazione di orbite circolari: ricavarsi la terza legge di Keplero in tale approssimazione;
    • Osservare attentamente l'animazione di questa pagina web (purtroppo non tutti i browser sincronizzano bene le tre animazioni, provare eventualmente a ricaricare la pagina) e capire cosa rappresentano i diversi vettori.
  • Attività sperimentale (sebbene qualitativa o semiqualitativa): osservazione di Giove
    • Localizzazione del pianeta: si tratta di quella 'stella' enorme che domina nel cielo queste sere (verso Est subito dopo il tramono, quindi si alza).
    • Movimento relativo Terra-Giove: si fissi Giove ad una certa ora (ad es. alle 22:00), usando un qualche strumento (anche macchina fotografica con orientazione fissa puo andare bene) per registrarne la posizione:
      • nelle prossime settimane vedremo 'cosa succede' guardando Giove alla stessa ora;
      • cominciare a pensare (ed eventualmente a calcolare, ma senza andare subito a cercare la risposta in qualche almanacco) a cosa succederà nei prossimi mesi: al passare del tempo Giove alla stessa ora sarà a mano a mano più a Est o a Ovest?
    • Per chi ha un binocolo (non servono molti ingrandimenti, un 7× o 8× va più che bene, se è più potente e lo si usa senza cavalletto la situazione peggiora): osservazione delle 'lune' di Giove (ovvero dei suoi satelliti, che girano talmente velocemente da apparire in posizione diversa ogni sera):
      • sito che dà la posizione, istante per istante, delle 'lune' come sono viste dalla Terra:
        http://www.cielidolomitici.it/lune_di_giove.htm.
  Nota: Se questi (ed altri) 'compiti' verranno eseguiti regolarmente, potremo tenerne conto nel computo delle ore totali del corso.

---

 

Lezione 1 (20/10/10) [1 ora]

• Unità di misura astronomiche: Parsec, Unità Astronomiche, minuti luce.
• distanza Terra-Sole
• osservazione di Giove
  • dalla Terra: sincronizzazione degli orologi, ora locale, mezzogiorno locale
  • da due pianeti (ad esempio Terra e Marte): errori di parallasse
• longitudine, latitudine
• osservazione di fenomeni periodici dalla Terra (esempio: sorgere di una luna di Giove):
  • prima misura della velocità della luce (Romer)
  • effetto Doppler
• Note sull'importanza delle lune di Giove:
  • Scientifica/filosofica: altri pianeti hanno satelliti: contro sitema geocentrico;
  • Pratica: uso di orologi celesti (previa compilazione delle effemeridi su almanacchi) per sincronizzare orologi lontani;
  • Ricaduta scientifica delle misure di precisione: misura della velocità finita della luce.

Lavoro per casa: ripasso delle leggi di Keplero, in particolare ricavare la III legge dal moto circolare uniforme

Letture consigliate: (per dettagli vedi appunti dello scorso anno)

• Longitudine, Sobel
• L'isola Misteriosa, Verne

---

 

Lezione 2 (21/10/10) [3 ore]

• Esercizio: osservazione di un fenomeno periodico dalla Terra (ad esempio il sorgere di un satellite di Giove): come cambia il periodo a causa del moto di rivoluzione?
• Pendolo semplice:
  • Costruzione di un pendolo di lunghezza 1 m
  • misura del periodo (esercizio:correggere considerando anche il raggio della sferetta)
  • considerazioni sulle dimensioni della sferetta e forza di attrito
• Metro e secondo:
  • Definizioni moderne e storiche del metro e del secondo.
  • Paralleli e meridiani; latitudine e longitudine; polo ed equatore.
  • Giorno solare, giorno solare medio, giorno siderale e giorno di calendario.
    (esercizio:calcolare la differenza tra giorno siderale e giorno solare)
  • perchè il metro batte il secondo? (breve storia critica sulla nascita del metro, con ulteriori spunti di ripasso e di approfondimento)
• Esercizio:considerando un grave che cade in un "pozzo"che taglia diametralmente la Terra, che moto compie?
• Leggi di Keplero, dimostrazione della II.
• Basi di html.

---

 

Lezione 3 (25/10/10) [2 ore]

• Ancora su Giove, sue lune e questioni astronomiche
  (quant'è un pc? dimensioni della Galassia; quanto dista la stella più vicina?)
• Ancora sulla storia del metro, con spunti di riflessione e proposte di esercizi/approfondimenti correlati:
  • pendolo semplice; effetto della massa non puntiforme; barra oscillante.
  • Sulle unità di energia e di potenza: kw, HP (CV), kcal/h, Btu/h.
  • La 'magia' della pompa di calore:
    spunto di ripasso del ciclo di Carnot.
  • Dipendenza di periodo, velocità e velocità angolare dei pianeti in funzione della loro distanza dal sole.

 

---

Lezione 4 (28/10/10) [3 ore]

• Occhio alla luna, senza perdere di vista Giove.
  In particolare
  • notare come cambia la 'gobba nei prossimi giorni' a mano a mabo che “si avvicina al sole” (perché “gobba a levante, luna calante”?);
  • In particolare, si noti la configurazione Terra-Luna-Sole al quarto.
• Ancora pendoli e barre.
• Fine 'seminario' storico su metro (vedi dettagli su AA precedente).
• Un po' di meccanica:
  • 'Esperimento' di oggetto fermo tirato da elestico: cherchez les forces.
  • Non confondere coppie di forze (sulla stesso oggetto) che danno risultante nulla, con le copie azione-reazione.
  • Impulso <-> quantità di moto; lavoro <-> energia cinetica; quantità di calore <-> energia interna.
  • Un esercizietto: un oggetto, inizialmente fermo, cade da una certa altezza ed arriva a terra con vf = 4 m/s. Confrontare con il caso in cui parte con v0 = 3 m/s: → vf'?
• Uso del calibro; errori di lettura + intro a errori sistematici (“se non lavora a temperatura nominale?”)

 

---

Lezione 5 (4/11/10) [4 ore]

• Problemino di cinematica:
  • Oggetto lasciato cadere da una certa altezza e dopo un tempo t raggiunge la velocità di 4m/s. Altro oggetto viene lanciato a 3 m/s e lasciato cadere per lo stesso tempo t. Che velocità raggiunge?
    (Ricorda: Forza×Δx = ΔE_c, mentre Forza×Δt = Δp. Quindi una forza che agisce su uno spazio costante provoca una variazione di v², mentre una forza che agisce per un tempo costante prova una variazione di v.)
• `Lavoro' (nome di quel famoso integrale), somma dei lavori lungo i vari assi e relazione con prodotto scalare, variazione di 1/2 m v², 'invenzione' dei nomi energia cinetica e potenziale, relazione con energia termica (Mulinello di Joule).
• Esperimento: è più facile tenere in equilibrio su un dito un'asta lunga oppure una matita?
  • Cercare di collegare la spiegazione con le seguenti cose:
    • Dragster e la loro strana forma allungata.
    • L'asta di equilibrio che usano i funamboli.
    • Cosa succede quando accelero con l'auto? E quando freno?
    • Le auto di F1 (e le moto) hanno la trazione posteriore e i freni anteriori.
    • Ma allora perché alcune auto hanno la trazione anteriore? Maggiore guidabilità.
      • Carrello della spesa: è più facile spingerlo o tirarlo?
• Aristarco di Samo:
  • Stima delle dimensioni relative Terra/Luna dall'ombra proiettata sulla Luna durante un'eclissi (vedi ad es. questa foto
  • Stima della distanza Terra-Luna, osservando tempo di passaggio della Luna nel 'cilindro d'ombra' della Terra durante un'eclissi e trovando d_T.L./R_T = 60, in buon accordo con il valore attuale. (Vedi dettagli, ad esempio, qui.).
  • Distanza Terra-Sole mediante misura di triangolazione (quando la luna sta esattamente ad un quarto).
    (Nota: in questo caso il valore non venne corretto in quanto sarebbe servita una misura di angoli molto più accurata di qualla che poteva effettuare)
• Esperimento con righello lasciato cadere da uno studente e ripreso al volo da un altro:
  • misure di tempi di riflesso usando accelerazione di gravità (il righello viene lasciato cadere a sorpresa).
• Programma per la misura dei riflessi (compilato sotto Linux):
  • riflessi.c;
  • kbhit.c (gestione tastiera);
  • my_rand.c (gestione numeri casuali);
  • cercasi volontari per scrivere versione Windows, dove kbhit() dovrebbe esistere di default.
• Breve digressione su Galileo e le misure con il piano inclinato. Approfondimenti:
  • Galileo e l'esperimento del piano inclinato.
  • Ancora sul piano inclinato.
  • Galileo ed il pendolo (approfondito nelle lezioni precedenti).
• Introduzione a R come linguaggio franco per la didattica:
  -> Installarlo, provare a dare qualche comando e cominciare ad usarlo come 'calcolatore'.
  • Importanza del calcolo numerico e delle simulazioni.
  • Basi del linguaggio, 'help', vettori.
  • Per ora provare a studiare e far girare questo semplice script:
    • gittata.R
    provando magari ad aggiungere l'attrito.

 

---

Lezione 6 (8/11/10) [2 ore]

• Asta sospesa.
  • Polo in alto: analisi dei momenti e soluzione approssimata (piccole oscillazioni) dell'equazione dell'oscillatore armonico classico. Equilibrio stabile ad angolo nullo.
  • Polo in basso: equilibrio instabile ad angolo nullo.
    Proporzionalità inversa tra accelerazione e lunghezza dell'asta.
  • Dipendenza non lineare del momento di inerzia di un corpo rigido omogeneo dalle sue dimensioni.
    Esempi: sfera di raggio r e sfera di raggio 2r; barra di lunghezza 2l rispetto a barra di lunghezza l.
• Analogia gravità e elettricità (per corpi puntiformi).
  • Forza, campo, energia potenziale (andamento in funzione della distanza dalla sorgente), potenziale, potenza. (Vedi anche: Lezioni, in particolare §16.6)
  • Riduzione della formula generale dell'energia potenziale gravitazionale, alla formula valida a g costante (mgh).
    Sugli infinitesimi: senza ricorso allo sviluppo in serie di Taylor, ci si convince, attraverso semplici evidenze numeriche, che:
    1 / (1 ± ε) ≈ 1 ± (-ε)
    (1 ± ε)² ≈ 1 ± 2 ε
    (1 ± ε)^1/2 ≈ 1 ± ε / 2
    Esercizio: a livello dimensionale deve essere: E_p = α G M m / r. Imponendo che sia: E_p(R_T) = 0 → E_p(h)=mgh, verificare che α = -1.
• Elettricità.
  • Esistono generatori di tensione (si pensi alla pila).
  • Le differenze di potenziale si possono trasportare mediante conduttori.
  • Legge di Ohm.
  • Forza elettromotrice e lavoro della forza: analogia con un impianto sciistico di risalita:
    • potenza;
    • effetto Joule.
• Esercizio:

  dato il circuito a lato, con R1 = 45Ω, R2 = 10Ω, R3 = 10Ω, f1 = 2.1V, f2 = 1.9 V: calcolare le intensità di corrente nelle resistenze; assumendo VC = 0, calcolare VA, VB, VD; cosa succede se si spegne un generatore alla volta?

  Per la soluzione vedi qui.

 

---

Lezione 7 (11/11/10) [3 ore]

• Uso del teorema di Gauss
• Massa m all'interno della Terra:
  • Gli elementi di massa di ciascun guscio sferico omogeneo e concentrico con la superficie terrestre danno risultante delle forze nulla.
    • Questo può essere provato direttamente facendo l'integrale (per il caso generale vedi il teorema dei gusci, la cui dimostrazione è ovviamente fuori programma),
    • oppure si può pensare a tutte le coppie di elementi di massa opposte: ovunque sia m all'interno del guscio, la distanza viene compensata dalla diversa massa intercettata da coni opposti (vedi figura originale dai Principi di Newton, Sec. XII, prop. LXX, Th. XXX - il testo è una traduzione, in quanto notoriamente i Principia furono scritti in latino).
    • Semplice 'dimostrazione' della legge A prop. d² mediante lavagna luminosa.
• Circuito elettrico, maglie e nodi.
• Esempio di circuito con generatore (f=10V) con in serie R₁ (5Ω) e parallelo di R₂ e R₃ (10 e 8 Ω rispettivamente).
  Nota:
  • resistenze in serie: in ciascuna di esse circola la stessa corrente;
  • resistenze in parallelo: ai capi di esse c'è la stessa differenza di potenziale.
• Regole generali (leggi/principi di Kirchhoff) per 'risolvere' i circuiti:
  • Ad ogni nodo: Σ_i I_i = 0, con versi positivi per correnti entranti (e analogia idraulica);
  • Per ogni maglia: Σ_i ΔV_i = 0 (e analogia gravitazionale).
• Regoletta pratica per la legge delle maglie (ma è preferibile ricordare quella generale): Σ_i f_i = Σ_k R_kI_k, con f_i e I_k positive se sono nel "verso di percorrenza" della maglia (ovvero quello con cui si fa l'"inventario delle differenze di potenziale", che non ha niente a che vedere con i versi delle correnti!).
• Bilancio energetico di circuito elementare costituito da generatore e resistenza (ed analogia gravitazionale/idraulica):
  • lavoro compiuto dal campo elettrico e e dalla forza elettromotrice;
  • potenza necessaria per mantenere il circuito in funzione;
  • potenza fornita dalla forza elettromotrice e potenza dissipata dalla resistenza: Effetto Joule: P = I ΔV. (es. boiler)
• Partitore di tensione:
  • Resistori in serie di cui si conosce la tensione ΔV_s ai loro capi:
    • ΔV_i = ΔV_s V_i/(Σ_i R_i), proporzionale a R_i: cadute di tensione proporzionali ai valori delle resistenze;
    • resistenza equivalente della serie: R_s = Σ_i R_i (si sommano, quindi R_s > R_i);
    • giustificazione dei fili di collegamento come, approssimativamente, equipotenziali.
• Esempio di circuito un po' più complesso, con due generatori e tre resistenze. Indicando quattro punti ai vertici di un rettangolo, con A in alto a sinistra e gli altri (B, C e D) in senso orario:
  • R₁ = 45 Ω fra A e C;
  • R₂ = 10 Ω fra B e C;
  • R₃ = 10 Ω fra C e D;
  • f₁ = 2.1V fra A e B, orientato verso A [ovvero V (A) > V (B)];
  • f₂ = 1.9V fra A e D, orientato verso A.
    • Risoluzione dell'esercizio con le equazioni di maglie e nodi;
    • calcolare le correnti I₁, I₂ e I₃ che scorrono nei resistori;
    • cosa succede se si pongono a zero, alternativamente, le tensioni ai capi dei due generatori? Valutare le nuove correnti e confrontare con quelle prodotte dai due generatori entrambi 'accesi'.
• Semplici misure elettriche:
  • resistenza di collanina di resistori cortocircuitati agli estremi;
  • partitore di tensione.
• Multimetro analogico ICE: principio di funzionamento e modalità d'uso.
  • Schema per amperometro e voltmetro a pag. 1 di questo documento pdf.
  • Resistenza interna in modalità amperometro e voltmetro.
  • Perturbazioni introdotte dagli strumenti. Voltmetro ideale (R_V → ∞) e amperometro ideale (r_A → 0).
• Esperienza del partitore eseguita con un voltmetro di resistenza interna paragonabile a quella `tipica' delle resistenze della `collanina'.
• Magari provare a graficare alcuni di questi risultati (ad esempio con R).
• Inoltre:
  • Il primo quarto della luna si verifica sabato 13 novembre ore 16:40 (Aristarco!!)
  • Perché “gobba a ponente, luna crescente”? (Prevedere/osservare posizione relativa sole-luna durante i prossimi 10 giorni)
  • Cielo nel mese di novembre

 

---

Lezione 8 (15/11/10) [3 ore]

• Esercizio: Centro di massa e mediana: le 3 mediane di un triangolo si incontrano nel baricentro.
  (dimostrazione elementare con un triangolo tagliato a "fettine", il baricentro passa sempre per il punto medio delle "fette")
• Forze di attrito:
  • differenza tra attrito statico e dinamico.
  • metodo delle aree per trovare graficamente variazione di velocità (Δv) e variazione di posizione (Δx) (vedi anche appunti fisica per informatici pag 6)
  • Esercizio:trovare le formule del moto uniformemente accelerato a partire dal grafico con a = cost usando il metodo delle aree.
• Esercizio: Si considerino due particelle che partono all'istante t =0 con velocit? v₀ e accelerazioni a₁= 1 m/s² e a₂= 0 m/s². Negli istanti successivi a₁ decresce mentre a₂ cresce linearmente nel tempo, fino a che all'istante t₁ vale che a₁=0m/s² e a₂=1m/s²
  • All'istante t₁ quale delle due va più veloce?
  • Quale delle due va più lontanto?
  
  
  Risolvere con il metodo delle aree
• Lavoro della forza di attrito e della forza peso: F_att compie sempre un lavoro negativo (vedi appunti fisica per informatici pag 49)
• Esperimento: determinazione della forza di attrito statico usando una massa su un piano di cui si fa variare l'inclinazione.
• Ricorda: la F_{att statico} a differenza di F_{att dinamico} non ha una "formula fissa": il coefficiente di attrito statico μ_s serve per determinare la forza massima.
• Sapendo che la F_{att statico} è uguale e opposta alla componente della forza peso lungo il piano si ricava che μ_s= tg ϑ_max, dove ϑ_max è l'angolo per cui la massa inizia a muoversi.
• Esperimento: Prendendo una scopa (lunghezza L) e sospendendola su due dita tenute alla stessa distanza da L/2 (attenzione!non dal baricentro), se si prova ad avvicinare le dita si verifca che si muove solo quella pi? lontanta dal centro di massa, perché F_{att statico} è minore. L'attrito dinamico aumenta al diminuire della distanza dal baricentro, ad un certo istante (quando le due forze di attrito sulle dita sono uguali) si muove anche l'altra mano e le due si incontrano proprio nel baricentro.
• Attrito viscoso: F_{att viscoso}= -βv
  • Analisi dell'attrito viscoso nell'aria : osservando il moto di un fazzoletto lanciato in aria si nota che ad un certo istante si raggiunge una situazione di equilibrio per cui la la velocità è costante:
    F_{att viscoso} e forza peso si bilanciano.
  • Nota bene: v_lim= mg / β --> la velocità dipende dalla massa perché F_{att viscoso} NON dipende dalla massa!
• Uso di R:
  • grafici di misure svolte con il multimetro la scorsa volta: collanine.R
  • grafici delle misure di riflessi: riflessi.R
  • gittata con l'aggiunta dell'attrito: gittata1.R
  • funzioni media e deviazione standard.
• Basi di statistica: Ripasso e chiarimenti
  • distribuzione di probabilità e distribuzione di frequenza.
  • medie pesate e valore atteso (attenzione, si parla di valore atteso solo per le distribuzioni di probabilit?)
  • analogie con le masse: se le probabilità (i pesi della media!) fossero masse il valor medio sarebbe il baricentro.
  • varianza e deviazione standard. Chiarimento sulla formula della deviazione standard (al denominatore N e N-1). Vedi anche dispense del docente (pdf
  )
  • analogia meccanica varianza- momento d'inerzia. Dall'espressione della varianza Var(x)= (x²)_m-(x)_m² analogia con teorema di Huygens-Steiner.

 

---

Lezione 9 (18/11/10) [3 ore]

• Asta tenuta con due dita (variante dello scopettone)
  • avvicinandole all'inzio un solo dito si muove; poi dopo una certa distanza x si ferma e comincia a scorrere l'altro dito.
  • A partire dell'esperimento valutare il rapporto tra i coefficienti di attrito statico e dinamico: si provi a fare il conto assumendo x/l = 0.9, ove l è la lunghezza totale (e assumendo che le due dita erano inizialmente alle estremità del 'bastone').
• Problema sulla falsariga di quello della precedente lezione:
  • Due palline percorrono, partendo dalla stessa altezza con v=0, rispettivamente un quarto di circonferenza ed un "ramo di iperbole" finendo il proprio percorso nello stesso punto:
    • Con quale velocit? arrivano? La stessa! (basta scrivere l'energia iniziale e finale)
    • Chi arriva prima? La pallina che percorre il ramo di iperbole (pensare ai casi limite).
• Piano inclinato:
  • Misura del coefficiente di attrito statico dall'angolo di 'stacco'.
  • Confronto fra discesa di pallina (o cilindro) che ruota senza scivolare e corpo che scivola: chi arriva prima?
  • Considerazioni energetiche e implicazioni sulla velocità finale.
    • Per entrambi in partenza: E₀ = mgh
    • Alla fine:
      • Corpo: E_f^pm = mv_pm²/2
      • Pallina: E_f^pall = mv_pall²/2 + Iω²/2
    • Quindi la pallina arriva con una velocit? minore.
      • Usando v = ωR (R, raggio pallina) si ottiene: E_f^pall = (mv_pall²/2)*(7/5) (non dipende da R!)
  • Tabella di analogie fra moto traslazionale e moto rotazionale intorno ad asse fisso.
• Circuiti:
  • Principio di sovrapposizione e sua utilità.
  • Teorema di Thevenin
    • Dimostrazione "a fumetti".
    • V_eq = 'V₀' = V_AB (tensione misurata a circuito aperto); R_eq = R_AB ; I_cc = V_eq/R_eq
    • Esercizio: V_AB=5V; I_cc=5mA; alla scatola nera ? collegata una resistenza da 1kΩ. Quanto valgono I_R e V_AB' ?
  • Multimetro ICE come ohmmetro.
    • Differenze tra 'calibrazione' e 'settaggio'.
• Termologia
  • Temperatura e Calore.
  • Termometro
    • Come sono legate le dimensioni del bulbo con la 'sensibilità'?
      dh/dT = (V₀α_V)/A
    • Principio zero della termodinamica; temperatura di equilibrio: media pesata con le capacità termiche → Att. il termometro può perturbare il sistema.
  • Grafico di temperatura, in funzione del tempo, dall'acqua da temperatura sotto lo zero (ghiaccio) all'ebollizione; significato dei punti stazionari (ad applicazione nella cottura...) e delle diverse pendenze sotto e sopra lo zero;
  • Calore latente di fusione ed ebollizione: concetti e principi di misura (e precauzioni nell'eseguire l'esperimento: stratificazione di temperatura dell'acqua scaldata dal basso!).
  • Capacità termica e calore specifico (e parallelo tra altri tipi di capacità: ad esempio capacità elettrica).
  • Caloria, definita come la quantità di calore necessaria ad elevare da 14,5 a 15,5 °C la temperatura della massa di un grammo di acqua distillata a livello del mare (pressione di 1 atm).
  • Esperimento: misura della potenza (effettiva) di un forno a microonde.
  • Altro esperimento (non terminato): processo di termalizzazione (raffreddamento del bicchiere d'acqua):
    • dai dati raccolti stimare la velocità di raffreddamento sia in °C/s che in cal/s e in Watt;
    • inoltre, assumendo una legge del tipo dQ/dt = α(T-T_A), ove T è la temperatura istantanea dell'acqua e T_A la temperatura ambiente, stimare il coefficiente dimensionale α.
• Esperimento del dito immerso in acqua in un recipiente posto su una bilancia:
  • spinta di Archimede e azione-reazione;
  • misura del volume (della parte immersa) del dito mediante la bilancia (!);
  • `tomografia' del dito da dP/dz, ove 'P' è il peso indicato dalla bilancia e 'z' l'affondamento.

 

---

Lezione 10 (22/11/10) [3 ore]

• Ancora Termologia:
• Densità dell'acqua (massima densità a 4 °C), dipende dalla temperatura
• Scambio termico con aria e acqua (c_{s acqua} > c_{s aria} e lo stesso vale per la costante di conducibilità termica). Esempio della sauna a 100 °C
• Sensazioni di caldo e freddo: esempio della sedia, il corpo è sensibile agli scambi di calore.
• Aggiunta di sale nell'acqua per aumentare il punto di ebollizione: per aumentarlo di 1 °C si devono aggiungere circa 60 g di sale. Esempio delle gelataie con ghiaccio e sale.
• Sui problemi della scorsa volta:
  • assumendo una legge del tipo dQ/dt = - α(T-T_A), α dipende da superficie, spessore della parete e una costante da cui dipende la dispersione termica.
  • considerazioni:
    • più è piccolo α e più lentamente avviene il raffreddamento/riscaldamento
    • il segno deve essere negativo: infatti se T < T_A il corpo si riscalda e dQ/dT è positivo, viceversa se si raffredda.
  • Usando sempre la stessa legge possiamo vedere la variazione di T nel tempo:
    Essendo dQ=CdT si ottiene dT/dt= - α/C(T-T_A)
  
  
  • Raffreddamento/Riscaldamento del termometro:lo strumento ci mette un certo tempo per arrivare a regime: si può giocare sul fattore α/C, ad esempio mettendo un cappuccetto di gomma sul bulbo in modo che la velocità dT/dt con cui varia la temperatura sia più piccola.
• Passando ad alcuni problemi apparentemente diversi fra di loro e con la termalizzazione:
  • Carica del condensatore:
    
    usando la legge di Ohm ai capi di R:
    
    I=(f -V_c)/R= dq/dt=dQ/dt
    dove q è la carica che fluisce nella resistenza e Q la carica che viene immagazzinata nel condensatore.
    Da questa, essendo Q=CV_c si ottiene
    dV_c=-1/RC(V-f)=-1/RC(V-V_fin)
  • Corpo frenato da attrito di viscosità proporzionale alla velocità con coefficiente di proporzionalità β. Con i soliti simboli per forza, massa e velocit?, considerando che la forza motrice sia la forza peso otteniamo:
    mg - β v = m dv/dt
    da cui dv/dt= - β (v-v_f)/m
    • Esercizio: quanto può essere v_fin per un paracadutista? Basta stimare un'altezza massima sostenibile all'impatto.
  • Osservando le equazioni scritte si hanno 3 fenomeni che seguono la stessa equazione differenziale:
    
    dz/dt = - (z - z_A) / τ
    
    
    • E' un'equazione a variabili separabili. Integrando si ha -> ln (z(t)-z_f ) = ln ( z₀-z_f) - t / τ
    . Linearizzazione su carta semilog
    • significato di τ
    • Come si può trovare la soluzione in maniera elementare? Provare a sostituire le derivate con dei delta e costruire una successione, as esempio T(n) a partire da T(₀+Δt) =T₀ + ΔT
      • Problemi
        • Usando i valori di temperatura iniziale dell'esperienza del bicchiere d'acqua nel microonde e il parametro α stimato dalla velocità iniziale di raffreddamento, valutare T(n) in modo numerico, ad esempio mediante R.
        • Più in generale, assumendo z₀ diverso da zero e z_F uguale a zero (ad esempio scarica del condensatore):
          • ricavarsi la legge geometrica di decrescita di T(n);
          • fare il limite per Δt → 0 e mostrare che T(t) segue una legge esponenziale negativa.
  • Probabilità:
    • Introduzione al problema delle `sei scatole' dalla quale ne è stata estratta una a caso: probabilità della composizione della scatola e probabilità di estrarre da essa una pallina bianca;
    • Confronto con scatola di composizione nota (5W, 5B): paradosso di Ellsberg.
    • Imparare le cause dagli effetti: problema fondamentale del metodo sperimentale di Poincaré.
    • Ripasso della distribuzione binomiale (vedi dispense PRO): essendo p= probabilit? di successo e n = numero di prove
      • E[X]=np
      • &sigma (X)= (np(1-p))^1/2
      • frequenza relativa: f(n)= X/n. Corrispondenza tra frequenza relativa e probabilit?
      • Teorema di Bernoulli (“legge” dei grandi numeri - attenzione al termine “legge”, che induce ad errate interpretazioni): E[f_n]= E[X]/n = p, &sigma(f_n)= (p(1-p)/n)^1/2 → maggiore è il numero di prove che prevediamo di fare e maggiormente f_n si avvicina a p.
        • A proposito del recupero dei numeri ritardatari: vedi qui.
        • (E qualcuno può essere anche interessato ai sistemi per vincere al lotto (l'unico modo per vincere al lotto è ... organizzarlo.)
    • Problema dell'ubriaco: Distribuzione geometrica (vedi dispense PRO )
      E[X]=1/p non è il valore più probabile ma il punto dove si addensano le misure. In questo caso il valore più probabile è il primo! (la soluzione del problema dell'ubriaco è il primo tentativo!)
    • Non si confonda valore atteso con più probabile!
    • Concetto di probabilità: legato a "quanto crediamo".

 

---

Lezione 11 (25/11/10) [3 ore]

• Processo di termalizzazione (e analoghi processi in cui la variazione per unità di tempo di una grandezza è proprzionale al valore istantaneo della grandezza stessa):
  • come ottenere la soluzione in maniera elementare, qui, mediante una progressione geometrica che nel limite di Δt → 0 tende a esponenziale:
    • simula_termalizzazione.R (con linearizzazione dell'andamento esponenziale mediante ordinata proporzionale al log della grandezza fisica).
• Breve ripasso di idrostatica
  • Rivedersi: principio di Archimede e legge di Stevino.
  • Misura di volume per immersione: provetta stretta → maggiore sensibilità.
  • Esercizio: in una piscina si trova “una barchetta con a bordo una persona con una pesante incudine. Se ora la persona getta nella piscina l'incudine, come varia il livello dell'acqua?”
    (Come esperienza didattica si può pensare ad una scodella di plastica, con dentro un pesetto, che galleggia in una scodella/bagnarola)
• Probabilità
  • Definizione di Probabilità come "grado di fiducia", slides (verso la fine)
  • Regole di base della probabilità, slides
  • Probabilità legata allo stato di informazione del soggetto che la valuta: è soggettiva.
  • Probabilità sempre condizionata [in particolare, commenti sul significato della formula P(A|B)=P(A,B)/P(B)]
  • Ripasso su regole della probabilità [gli argomenti trattati si trovano nei capitoli 1,2,3 (non fondamentale), 4 delle dispense "Probabilità ed incertezze di misura" (Parte 1: PDF)]
  • Funzione di probabilità [f(x)] e funzione cumulativa [F(x)]
  • Le possibilità dei lanci di due dadi (somma e sottrazione) sono in un 'quadrato' (piano cartesiano).
    • Distribuzione triangolare discreta;
    • Estensione al caso continuo.
  • Generatore di numeri pseudocasuali a partire da 'runif()'.
    • Metodo 'hit/miss' (in pratica estraggo in un 'rettangolo').
      • simula_binomiale.R mediante hit/miss.
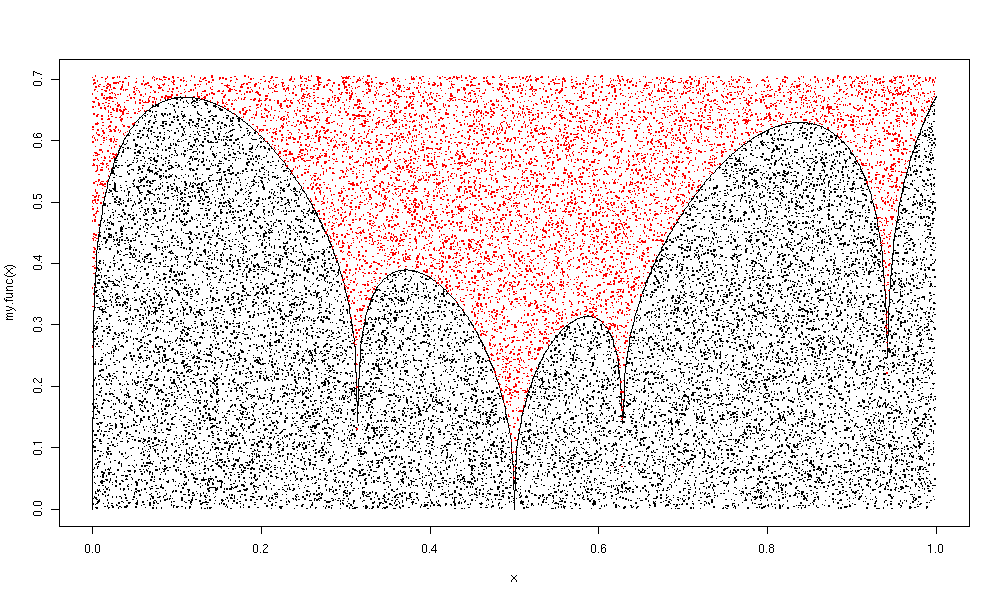
      • simula_funzione_strana.R mediante hit/miss (facendone anche l'integrale!):
        • risultato dei `tiri':
    • Altrimenti si può usare il metodo di inversione della funzione cumulativa: guadagno in efficienza (pensa ad esempio all'esponenziale > 'rettangolo' infinito!) e se la funzione cumulativa è invertibile è molto facile da usare.
      • simula_esponenziale.R mediante inversione della cumulativa.
  • Processo di Bernoulli, distribuzione geometrica e distribuzione binomiale.
  • Distribuzione di Poisson: limite della binomiale per p → 0, n → infinito, np=finito (=λ);
  • Processo di Poisson, con i due `punti di vista':
    • numero di conteggi per tempo di misura prefissato: → poissoniana;
    • tempo in cui accade il primo conteggio: → esponenziale;
    • simulazione: processo_di_Poisson.R: genera i tempi di accadimento, analizzando poi gli intervalli di tempo fra accadimenti successivi e i nr di accadimenti in intervalli di tempo di lunghezza prefissata.
• Infine, si ricorda che un buon editor per programmazione (e quindi anche editare file html, ad esempio capisce la sintassi e colora opportunamente il testo) è emacs: vedi qui.

 

---

Lezione 12 (29/11/10) [3 ore]

• Ancora sulla Termalizzazione:
• Come aumentare artificialmente la costante di tempo di un termometro;
• Proposte di attività sui dati sperimentali di termalizzazione:
  • grafico di ΔT/Δt in funzione della temperatura, per mostrare che la termalizzazione segue la legge ΔT/Δt=-α(T-T_A);
  • oppure, assumendo questa legge, valutare α a diversi tempi.
• analisi numerica dell'andamento T(t), a partire da temperatua iniziale e α valutato sperimentalmente (spiegazione dello script simula termalizzazione.R )
• Linearizzazione:
  • l'andamento di log(T-T_A) è lineare nel tempo --> attenzione! Non l'andamento di log(T)!
  • la pendenza del grafico è l'inverso di un tempo, e corrisponde a -1/τ
  • se si cambia la base del logaritmo (es. da ln a log₁₀) cambia la scala ma non l'andamento, infatti nel cambio della base c'è solo un fattore moltiplicativo.
  • linearizzazione di una legge di potenza: y=√x -> è lineare l'andamento di y² su x.
  • Scale logaritmiche: invece che calcolare di volta in volta i logaritmi si può “comprimere” la scala in modo logaritmico
  • Carte semilog: costruzione del grafico log(T-T_A) vs t usando i dati simulati (script sopra menzionato).
  • Fluttuazioni statistiche: costruzione del grafico con R considerando anche un errore percentuale gaussiano (sigma.p=0,02 e sigma.p=0,05)
  • stima della costante τ dall'opposto del reciproco della pendenza, ricordando che la grandezza che linearizza è il log della differenza:
    m = Δlog/Δt → per calcolare il Δ si prendono i punti sulla retta e si scelgono quelli più facilmente leggibili
  • Carta doppio log:
    • linearizzazione di leggi di potenza:
      log y = log y₀ + α log x → y = y₀ x ^α
    • la pendenza rappresenta la potenza:
      α = Δlog(y)/Δlog(x).
• Ancora sui generatori di numeri casuali:
  • Analisi dello script simula_funzione_strana.R
  • Contando i pallini neri e quelli rossi:
    N.neri/(N.neri+N.Rossi) = Rapporto delle aree → si trova l'integrale della funzione!
  • problema: che incertezza associare al valore di integrale ottenuto? (chiaramente, le cose sono diverse se facciamo 100 tiri casuali nel rettangolo o ne facciamo 1000000.
    → ci ricolleghiamo così ad un altro problema:
• Per introdurre l'inferenza probabilistica (bayesana), affrontiamo il problema del biliardo (Thomas Bayes, 1763).
  • Su un tavolo da biliardo largo l si tira una palla, che si ferma in un punto P.
  • Immaginando di tracciare una retta r passante per P, perpendicolare a l, l'area del tavolo si può pensare divisa in due porzioni (a sinistra di r e a destra di r).
  • Si toglie la palla dal tavolo, si eseguono altri tiri e per ognuno si dice se la palla lanciata si è fermata a sinistra o a destra di r.
  • Da queste informazioni si deve inferire dove si è fermata la palla iniziale rispetto a l (cioè in che punto r interseca l): il risultato sarà una p.d.f. di r, ovvero f(r), dalla quale si valuterà un valore più probabile, un valore atteso (`previsione' probabilistica), una deviazione standard ('incertezza di previsione') e tutti gli eventuali intervalli di probabilità di interesse.
  • Dal biliardo di Bayes all'area della “funzione strana.
• Carica del condensatore.
  • Costruiamo un circuito RC serie in corrente continua (R = 30MΩ, C = 2,2μF, f = 4,52V; basetta multifori; multimetro Flucke).
  • Misuriamo la differenza di potenziale ai capi del condensatore che si carica (stato iniziale: circuito aperto).
  • Osserviamo che non si carica a 4,52V, ma a circa un quarto di tale valore;
    se usiamo il voltmetro economico la cosa peggiora!
    se stacchiamo il voltmetro, la tensione sale verso quella del generatore (`ipotizziamo', in quanto non la possiamo osservare), ma ridiscende da dove era arrivata quando riattacchiamo lo strumento (e questo si vede).
  • Perturbazione degli strumenti di misura:
    • il voltmetro reale ha resistenza interna R_V e quando il condensatore è carico, R e R_V sono in serie si ha un partitore di tensione (tanto per ricordare che il concetto di serie non è puramente geometrico).
  • Esercizi: con i dati ottenuti:
    • calcolare misurare per via grafica la costante di tempo del circuito (τ attesa da `RC': 66s), ricordando che la carta semilogaritmica linearizza la legge esponenziale;
    • valutare (ovvero misurare) la resistenza interna dei due voltmetri;
    • provare a valutare le costanti di tempo `reali' tenendo conto delle resistenze interne del voltmetro;

 

---

Lezione 13 (2/12/10) [4 ore]

[Speciale lezione/seminario/esame]

• Quinconce di Galton (`pallinometro') e suoi problemi logici e costruttivi (a proposito, la struttura a quinconce è quella tipo 'cinque di denari').
  [Per questa assurdità didattica vedi anche apposito capitolo delle dispense Le basi del metodo sperimentale, ove sono anche riportati dei dati simulati per il caso a due file di chiodi.]
  • E' un Processo di Bernoulli dove il successo (sx) vale +1 e l'insuccesso (dx) vale -1.
  • Dati x (numero successi), n (numero di file) ed i (punto di ingresso):
    • il punto di uscita u è : u=i+2x-n
    • valore atteso: E[u]=E[i]+2E[x]-E[n]=i+2pn-n=i (p=1/2)
    • σ[u]=2σ[x]=√n
  • Problema: conoscendo il punto di uscita della pallina, sono in grado di indicare il punto di entrata?
    Imparare le cause dagli effetti
    • Ci sono ipotesi più probabili (ma attenzione agli effetti di bordo; inoltre la distribuzione dei punti di partenza potrebbe non essere uniforme).
• I due problemi delle 'tre scatole', con conduttore e due o un solo giocatore: rilevanza dello stato di informazione per la valutazione della probabilità (la mera descrizione della situazione fisica non è sufficiente).
  La variante con un solo giocatore è nota come Monty Hall problem,
  • una eccellente spiegazione del quale (anche se la fa un po' lunga) si trova su YouTube,
  • mentre su questo spezzone dal film 21 il problema non ha soluzione univoca, in quanto il prof. non dice esplicitamente che il conduttore ha intenzione di aprire una porta con una capra (anche se la cosa potrebbe essere sottintesa, in quanto dice almeno che sa dov'è il premio).
  • È molto facile incontrare gente (o pubblicazioni) che formulano male il problema e poi pretendono che la soluzione corretta sia quella di cambiare! - vedi ad esempio
    • quella che sembra la prima formulazione che ha raggiunto il grande pubblico (si dice che sa, ma non anche che vuole);
      (per l'attuale versione ufficiale del problema, inclusi interessanti commenti vedi qui.)
    • il volumone Introduction to probability, sponsorizzato dall'American Mathematical Society (versione pdf, vedi pag. 137).
      (Se la citazione dal Parade Magazine riportata nel libro è corretta, sembra che nella prima versione del problema non era detto nemmeno che sapeva e che “Marilyn clearly expected her readers to assume that the game was planned in this manner”...).
  • Una buona spiegazione del Monty Hall è anche contenuta ne Lo strano caso del cane ucciso a mezzanotte, di Haddon Mark, un libro assolutamente raccomandabile, soprattutto ad insegnanti di matematica e fisica, per le pregevoli chicche ivi contenute:
    • Recenzione della Mathematical Association of America.
• Problema delle 'sei scatole' dalle quali ne è stata estratta una a caso:
  • Per una contestualizzazione del problema vedi articolo sulla Treccani online.
  • probabilità della composizione della scatola
  • probabilità di estrarre da essa una pallina bianca: P(b|S<sub>i</sub>)
    • P(b) = P(b|S<sub>0</sub>)*P(S<sub>0</sub>)+...+P(b|S<sub>5</sub>)*P(S<sub>5</sub>) = P<sub>0</sub>*P(S<sub>0</sub>)+...+P<sub>5</sub>*P(S<sub>5</sub>) = 1/2 (media pesata)
    • P(S<sub>i</sub>|b)=P<sub>i</sub>/3
    • P(b|b<sup>(1)</sup>)=P(b|S<sub>0</sub>)*P(S<sub>0</sub>|b<sup>(1)</sup>)+... = 0<sup>2</sup>/75+1<sup>2</sup>/75+...+5<sup>2</sup>/75 = 11/15 (quadratica!)
      • P(b|I(t)) → P(b|I<sub>0</sub>,b<sup>(1)</sup>) → P(b|I<sub>0</sub>,b<sup>(1)</sup>,b<sup>(2)</sup>) → P(b|I<sub>0</sub>, dati sperimentali)
  • Complicazioni del problema:
    • osservazione mediata da 'intermediario' che può mentire (es. strumento): O<sub>i</sub>->R<sub>i</sub>, ove O<sub>i</sub> e R<sub>i</sub> stanno, rispettivamente, per osservazione i-ma e 'report' i-mo.
    • incertezza sullo stato di preparazione: Prep->Box, ove i possibili 'stati' (modi) di Prep sono 'uniforme' e 'binomiale'.
  • Simulazioni di sequenze mediante R:
    • Confronto P(W|dati) con f=#W/#ntot (frequenza relativa)
  • Introduzione alle Reti bayesiane:
    • Problema delle sei scatole, con variazioni sul tema, analizzato mediante la Versione lite (gratuita, con funzionalità limitata) di HUGIN:
      • differenza fra 7 osservazioni W e 7 report W;
      • probabilità di 'mentire' dipende non solo dalla prob. di mentire del singolo intermediario, ma anche da cosa hanno detto gli altri (!);
      • prob. della composizione della scatola e dei modi di preparazione a seconda che si abbia l'informazione dei colori veri delle palline o i loro 'report';
      • caso di 6 report W e 1 B, confrontato con 6 report W e 1 'colore certo' W.
      • ...
      • Per un problema analogo a quello delle scatole con file di Hugin scaricabile, vedi appendice J di articolo ispirato al tenente Colombo.
    • Altro software per reti bayesiane:
      • programma 'open source' (con pro e contro rispetto a HUGIN): JavaBayes
      • un altro programma commerciale, con una funzionalità simile a quella di HUGIN e di cui esiste altrettanto una demo scaricabile (solo versione per Windows, ma funziona bene anche sotto Linux mediante Wine): Netica.
  • Estensione da 6 a 101 scatole (o numero arbitrario grande)
  • Passaggio al continuo:
    • inferenza del parametro p della binomiale (“inferenza parametrica”)
      • teorema di Bayes per variabili continue;
      • caso di prior uniforme;
      • f(p|n,x), valore atteso e varianza di p; regola di successione di Laplace; significato di E[p]: vedi dispense.
      • Simulazione in R biliardo di Bayes: biliardo_bayes.R (qualcuno può aiutare a migliorare la grafica?).
      • Esercizi:
        • Viene effettuato un esperiento simulato del biliardo di Bayes, con 1000 lanci e ci viene detto che la palla è finita 192 volte `a sinistra' e 808 `a destra'. Dove si era fermata (con incertezza standard) la palla lanciata inizialmente?
        • Viene eseguita una stima con metodo di Monte Carlo della `funzione strana' (vedi lezioni precedenti), ottenendo il seguente risultato: 20023 volte il punto generato finisce sotto (o tocca) la curva; 9977 volte il punto finisce sopra. Sapendo inoltre che l'ascissa era generata uniformemente fra 0 e 1 e l'ordinata era generata uniformemente fra 0 e 0.7045316 ('fmax'), stimare l'integrale fra 0 e 1 della `funzione strana' (inclusa l'incertezza standard).
• Teorema di Bayes
  • P(H|E)= P(E|H)*P(H) / P(E)
  • P(H<sub>j</sub>|E) è proporzionale a P(E|H<sub>j</sub>)*P(H<sub>j</sub>) (manca normalizzazione)
    • prior (probabilità a priori);
    • posterior (probabilità a posteriori);
    • P(E|H<sub>i</sub>) ('likelihood', o verosimiglianza - attenzione!).
  • Interessante riscrittura:
    P(H|E)/P(H) = P(E|H)/P(E)
    • ad esempio analizzare come varia P(b|H<sub>i</sub>)/P(b).
  • Per familiarizzarsi, si raccomandano i problemi del capitolo 5 delle dispense di probabilità.
• A proposito di `statistica' e statistica bayesiana, vedi contributo a Scienza per tutti dei Laboratori Nazionali di Frascati.

 

---

Lezione 14 (9/12/10) [3 ore]

• Analogia pallinometro e random walk
  • Pallinometro nello spazio del tempo per il moto browniano: σ della binomiale va come radice di n → σ del moto browniano va come radice del tempo.
  • Pallinometro nello spazio dei soldi per il gioco d'azzardo (cenni al problema della rovina del giocatore)
  • Pallinometro nello spazio delle velocità (o dei momenti) per i fenomeni di diffusione.
    • Iniettiamo una particella inizialmente ferma nella materia. Gli urti che subisce sono il random walk nello spazio delle velocità. In prima approssimazione, gli urti contribuiscono, in media, tutti allo stesso modo. Per simmetria, il valore atteso della velocità è 0, la deviazione standard è quella della teoria cinetica dei gas, perché la velocità tende al valore di regime (velocità quadratica media). Dopo un certo numero di urti, la distribuzione di ciascuna componente della velocità è gaussiana. La distribuzione del modulo della velocità è maxwelliana.

Bibliografia:

• Moto browniano, pallinometro ed errori di misura
• Distribuzione di velocità delle molecole di un gas perfetto

• Ancora sui problemi di probabilità inversa (quella dei problemi della fisica)
  • Il pallinometro ancora si presta.
  • Problema dell'AIDS.
    • Attenzione a non dare per scontato che le prior di un problema siano uniformi.
    • Commento sulla normalizzazione: nelle probabilità relative il coefficiente di normalizzazione si semplifica, ma non solo, la formula di Bayes è tale che si possono confrontare anche eventi non complementari (non è necessario che formino una classe!)
    • Mettiamo la formula di Bayes nella forma: (posterior odds) = (Bayes's factor) x (prior odds)
    • Test in cascata: più analisi indipendenti ^(*) eseguo, più ho ragione di credere al risultato <=> le posterior odds sono via via maggiori, perché si moltiplicano i fattori di Bayes.
      [^(*) Indipendenza probabilistica ('stocastica') fra A e B sta ad indicare che la probabilità di B non cambia se si ipotizza A (e viceversa): non è ovvio che due analisi “indipendenti” fatte in laboratori diversi siano veramente probabilisticamente indipendenti!]

• Passaggio al continuo:inferenza del parametro p della binomiale (vedi lezione scorsa)
  • applicazione del teorema di Bayes in modo sequenziale
  • Caso di prior uniforme ( f₀=k) come ad esempio per il biliardo di bayes
  • f(p|nx), valore atteso e varianza di p
  • regola di successione di Laplace
    • Esercizio: ricavarsi tale regola, ovvero P(E | n successi su n prove) = (n+1)/(n+2), calcolandosi prima f(p) sotto tali ipotesi (+ prior uniforme) e ricordandosi che P(E) è pari al valore medio di p pesato con f(p).
  • Esempi numerici della scorsa volta: biliardo di Bayes e funzione strana
  • incertezza standard come σ della pdf inferenziale sulla variabile di interesse.
  • parentesi sulle cifre significative
• Ripassare distribuzione di gauss
• Teorema centrale del limite
  • Combinazione lineare di variabili casuali, valore vero e varianza
  • dimostrazione "a fumetti" del teorema
  • Generatore di numeri pseudocasuali gaussiano a partire da 'runif()'
  Bibliografia (si ricorda che la maggior parte di queste cose sono assunte note da corsi precedenti):
  • Valore atteso di una funzione di una variabile casuale
  • Proprietà formali di varianza e deviazione standard
  • Riepilogo di alcune proprietà delle funzioni di variabili casuali
  • Teorema del limite centrale
  • Simulazione di numeri aleatori distribuiti secondo una distribuzione normale
• Esercizio:
  caso di risposta gaussiana dello strumento.
  • Sapendo che f(x) è descritta da una gaussiana di valore μ incognito e σ noto esattamente, determinare f(μ|x1), ove x1 è un valore osservato (partendo da una prior su μ uniforme);
  • con il solito uso sequenziale del teorema di Bayes, determinare f(μ|x1,x2,...) da una sequenza di osservazioni x1, x2, etc., usando ad esempio (per poter controllare i risultati) i seguenti valori : 2,5-1,7-1,9-2,8-2,1-2,5-1,1-2,8-2,5-2,1.

 

---

Lezione 15 (13/12/10) [3 ore]

• Risoluzione esercizio in rosso della scorsa lezione (regola di successione di Laplace nel caso di n successi su n prove).
  • Caso più generale (n prove, x successi):
    • funzione speciale Beta ...
    • e funzione densità di probabilità Beta:
      • L'avevamo già usata nel programma biliardo_bayes.R! [dbeta()]
      • Se si sceglie come prior generale una funzione Beta (prior coniugata, cioè strutturalmente della stessa famiglia della likelihood) la posterior é ancora una funzione Beta.
      • regola di riaggiornamento, usando la notazione di Wikipedia (in genere in due parametri vengono indicati con r e s) :
        • α_finale = α_iniziale + #successi
        • β_finale = β_iniziale + #insuccessi
• Inferenza di μ del campione gaussiano (nota σ=1)
  • E(μ)= x medio
    σ(μ)=σ/√n
  • Script in R: simple_inference.R
• Esperimento coperchio barattolo: da che parte casca?
  Problema asimmetrico e dunque la nostra mente dopo un paio di prove (con lo stesso risultato) é già certa di cosa uscirà alla prossima prova.
• Esperimento:
  Stima della densità di diverse palline.
  • Palline bianche (attenzione agli zeri accertati, anche se dopo la virgola):

    V (ml)	MTOT (g)
    68.1	0
    71.0	6.6
    73.9	13.2
    82.0	33.6
    90.3	53.8

  • Palline nere:

    V (ml)	MTOT (g)
    71.7	0
    74.5	6.9
    77.3	13.8
    87.0	37.3
    92.9	52.2

    (l'ultima misura é eseguita con alcune palline leggermente diverse)
  • Biglie:

    V (ml)	MTOT (g)
    52.0	0
    62.5	26.7
    73.0	53.6
    82.8	76.9
    91.9	97.8

    (alla fine é fuoriuscita qualche goccia)
  • Calibrazione:

    Bilancia "precisa" (g)	Bilancia laboratorio (g)
    300	299.8
    205.80	205.5
    150.31	150.1
    149.87	149.7
    10.61	10.5
    28.18	28.1
    34.63	34.6

  • Calcolare le densità e vedere se sono compatibili tra di loro.
  • Grafico di volume vs. massa (lineare, pendenza = 1/ρ).
• Fit
  • In R ? funzione lm(), ma attenzione alle scatole nere! (prima di usare un software, cercare di capire su quale principio si basa, come interpretare i risultati ed accertarsi che veramente risponda alla domanda che avevamo posto!):
    Ad esempio
    >  m <- c(0, 6.6, 13.2, 33.6, 53.8)
    >  v <- c(68.1, 71.0, 73.9, 82.0, 90.3)
    >  plot(m,v)
    >  fit <- lm(v~m)
    >  abline(fit)
    >  str(fit)    # per capire quanta roba c'è nell'oggetto 'fit'
    >  1/fit$coefficients[2]    # densità
    Esercizi: fare i vari fit con lm(), cercando di farsi una ragione dell'oggetto risultante ('fit' nell'esempio di sopra). Problema: come valutare le incertezze?
  • Modello lineare: μ_yi = m μ_xi + c
  • Rappresentazione con rete bayesiana (con link deterministici e probabilistici)
  • Caso generale e semplificazioni in caso di errore gaussiano solo su y e σ_y non dipendente da y e nota.
  • Plot in 3D: massimo di f(m,c|x,y) in corrispondenza dei valoci di m,c a cui crediamo di più.
    • Attenzione! Il massimo di f(θ₁,θ₂) potrebbe non coincidere con il massimo di f(θ₁) ed il massimo di f(θ₂).
  • Semplificazioni successive nei fit:
    • f(theta|dati) \propto f(dati|theta)× f₀(theta);
    • relazione lineare fra i valori 'veri': retta; due soli parametri;
    • errori solo sulle y;
    • osservazioni indipendenti: verosimiglianza congiunta prodotto di veromiglianze individuali;
    • prior uniforme: max della posterior è equivalente a massimizzare la likelihood congiunta (“massima verosimiglianza”)
    • errori gaussiani, noti a priori: massima verosimiglianza → “minimi quadrati” (con σ_i nella formula)
    • σ tutte uguali: → “minimi quadrati” `banale' (senza σ_i nella formula)
    Attenzione ai principi inutili!
    (Meglio attenersi alla teoria della probabilità.)

 

---

Lezione 16 (16/12/10) [3 ore]

• Misura della densità di un parallelepipedo di polistirolo:
  • come valutare le incertezze? il numero di cifre significative del risultato deve essere quello della misura meno precisa
  • Confrontando la sensazione di peso del parallelepipedo di polistirolo con delle masse note si osserva che questa à ingannevole: un po' come la diversa percezione fisiologica che si ha toccando oggetti alla stessa temperatura, ma aventi diverse conducibilità e capacità termica. Nel caso del peso la percezione è legata alla pressione sulla mano (oltre che alla tensione dei muscoli).
  • Nella misura della massa del parallelepipedo con la bilancia bisogna considerare che esso è immerso nell'aria e pertanto riceve una spinta di Archimede: la bilancia misura sempre la risultante delle forze applicate sopra
    • "Pesa più un kg di polistirolo o un kg di piombo?"
    • Se le due masse sono esattamente uguali, il polistirolo sposta un volume maggiore perciò la bilancia indica un valore minore
    • Se la bilancia viceversa indica uno stesso valore per entrambi la massa del polistirolo è maggiore di quella del piombo.
    • Quanto 'pesa' (nel senso di quanto ? 'massivo') un metro cubo di acqua? Uno di piombo? Uno di polistirolo?
      • Esercizio: Per quanto riguarda l'aria, ricavare il valore della densità dall'equazione di stato dei gas perfetti.
• Analisi dello script fit_densita.R
  • fit con R e confronto con formule note (vedi BMS pag 239).
  • Esercizio per casa: rifare lo script con le restanti misure per vedere se le densità vengono confrontabili
  • Spunto di riflessione Coefficiente di correlazione fra intercetta e pendenza (vedi dispense): che significato ha? che uso farne?
• Propagazione delle incertezze (vedi BMS pag 203 e ss. + dispense di probabilità [PRO])
  • Caso di combinazioni lineari:
  • Caso di funzione generica: linearizzazione intorno ai valori attesi
  • Caso di forme monomie e propagazione delle incertezze relative.
• Inferenza nel caso di σ ignota (vedi σ ignota).
  • Possiamo stimare σ dalla dispersione dei dati osservati intorno al loro valor medio.
  • Più rigorosamente possiamo scrivere l'inferenza bivariata e quindi marginalizzare su μ. Marginalizzando rispetto a σ inferiamo i valori di μ.
    • Ipotizziamo^(*) Facciamo uso di una prior uniforme in σ (imponendo σ positiva) e facciamo gli integrali con R (pdf non normalizzata / integrale = pdf normalizzata).
      [^(*)"Ipotizzare" dà l'impressione che la prior esista e siamo noi a non conoscerla.]
    • Script inf_gauss.R.
  • Osservazione sui risultati delle nostre analisi: ovviamente le incertezze nel caso di σ ignota devono essere maggiori di quelle nel caso di σ nota.

Inferenza trivariata e fit.

• f(m,c,σ|x,y) -> 3 dimensioni -> normalizzazione e 3 marginalizzazioni.
• Confrontare con i metodi approssimativi usati in fit_densita.R.

 

---

Lezione 17 (10/01/11) [2 ore]

• Confronto risultati densità palline assumendo σ nota (stimata con il metodo dei residui)
• Inferenza trivariata e fit nel caso di σ ignota
  • Facciamo uso di una prior uniforme (imponendo σ positiva)
  • f(m,c,σ|x,y) -> 3 dimensioni -> normalizzazione e 3 marginalizzazioni.
  • Significato del coefficiente di correlazione fra intercetta e pendenza
• Urti
  • La Quantità di moto di un sistema isolato è costante nel tempo.
  • Schematizzazioni generali: perfettamente elastico; perfettamente anelastico; anelastico (tutti i casi realistici sono per definizione non ideali).
  • Urto perfettamente anelestatico: si annulla l'energia meccanica nel centro di massa, il quale prosegue alla velocità che aveva prima dell'urto.
  • Urti elastici:
    • leggi di conservazione nell'urto perfettamente elastico;
    • caso unidimensionale (con sottocasi di particolare interesse):
      • legge dell'inversione della velocità relativa (o dell'uguaglianza delle somme delle velocità);
      • casi notevoli quando uno dei corpi ha massa 'infinita' (ovvero inerzia infinita e quindi non può cambiare velocità):
        • urto su pavimento o su parete;
        • urto di pallina da golf in movimento contro pallina da ping-pong ferma (e stima dei rapporti di velocità dalla distanza di caduta);
        • collisione frontale fra pallina da golf e pallina da ping-pong (e nuova stima...);
        • rimbalzo di pallina da golf con 'a cavallo' pallina da ping pong;
        • applicazioni calcistiche: colpo su palla ferma; colpo a seguire; contraccolpo; colpo 'accompagnato' (v pallone uguale a v piede);
        • Uovo messo in rotazione:
          • velocità iniziale di rotazione di uovo sodo e uovo fresco sono uguali (pari a quella delle dita);
          • l'uovo fresco acquista momento quantità di moto ed energia cinetica inferiore a quelle dell'uovo sodo; poi segue trasferimento a strati interni.
      • Altro caso notevole: masse uguali, urto frontale o di una in moto contro una ferma: soluzioni basate su uso di ragionamenti generali (simmetria del problema) e di trasformazioni galileiane delle velocità.
      • Alcuni gadget:
        • Simulazione di urti elastici ed anelastici
        • urti consecutivi di palline sospese (`pendoli di Newton');
        • versione 'sicura' delle `clic clac' (palline che schioccano, tipo queste, ma con bastoncini di plastica, invece degli spaghi, ruotanti intorno ad un asse): spiegazioni delle due 'soluzioni' (a parte quella banale di inseguimento).
  • Funzione dei guantoni nella boxe (nell'urto la variazione della quantità di moto avviene in un dt maggiore, quindi la forza applicata è minore)
  • Ottica geometrica.
    • Semplici esperimenti con proiettore (la sorgente), schermo e occhiali da vista, per stimare la distanza focale delle lenti attraverso la legge 1/p + 1/q = 1/f (nel caso p>>f di sorgente all'infinito):
      • lenti convergenti (da presbite): misuriamo la distanza tra lente e immagine a fuoco della sorgente sullo schermo, per tre occhiali diversi;
      • lenti convergenti in cascata: notiamo che la distanza focale diminuisce (la luce viene deviata due volte) e le diottrie si sommano;
      • lenti divergenti (da miope): misuriamo la distanza tra lente e immagine a fuoco della sorgente, che si forma tra sorgente e occhiale.
        • La diottria è l'inverso della distanza focale espressa in metri.
        • L'immagine reale si vede sullo schermo, l'immagine virtuale è quella che "si vede realmente"! [direttamente con gli occhi]
        • L'esperimento con materiale povero si dimostra qualitativamente significativo quanto uno eseguito con un banco ottico.
      Rifrazione della luce:
      • Innalzamento apparente del fondo (si pensi al fondo della piscina, alle gambe che al mare sembrano accorciarsi):
        • coloriamo il fondo di un bicchiere e lo osserviamo dall'alto, (circa) normalmente al piano dell'acqua, misurando la distanza a cui ci appare il fondo, rispetto al bordo: il rapporto tra profondità vera e profondità apparente è pari all'indice di rifrazione dell'acqua. Verificarlo.

 

---

Lezione 18 (18/01/11) [2 ore]

• Valore atteso e covarianza di variabili di output (Y _i) dat da combinazioni lineari di variabili di input ( X _i) indipendenti
  • Covarianza e coefficiente di correlazione: è vantaggioso usare ρ essendo adimensionale rispetto alla covarianza che può avere dimensioni "miste" e inoltre - 1 < ρ < 1
  • Caso semplice: Cov(X₁,X₂) = E [( X₁ - E [X₁])( X₁ - E [X₂])]
    per la linearit?: Cov( X₁,X₂) = E [ X₁ X₂] - E [ X₁] E [ X₂)]
    
  • A partire da questa si dimostra che se sono indipendenti Cov(X₁,X₂) = 0 : basta passare agli integrali, come conseguenza dell'ipotesi di indipendenza f ( X₁, X₂) = f ( X ₁ ) f ( X ₂) e perciò:
    E [ X₁ X₂] = E [ X₁] E [ X₂)] (vedi dispense PRO par 9.5.2)
  • Non è vero il contrario, cioò si possono avere due grandezze non indipendenti con Cov(X₁,X₂) = 0 e quindi ρ(X₁,X₂) = 0 --> esempio del "cratere"
  • Var(Y_l) delle variabili di output e Cov (Y₁,Y₂) (vedi dispense BMS par 11.4)
  • σ_lm = ∑_ij c _li c _mj σ_ij -->dove σ_lm= Cov( X_l,X_m) se l≠m e Var (X_l) se l=m
  • Anche se non c'è covarianza tra le variabili di input X _i pu? esserci covarianza tra le Y_i se queste dipendono dalle stesse variabili X _i
  • Notazione matriciale di varianze e covarianze
    • Per le combinazioni lineari: Y = C X dove C è la matrice dei coefficienti, X è il 'vettore' delle grandezze di input, Y è il 'vettore' delle grandezze di output
    • Per varianze/covarianze delle grandezze di output: V_Y = C V_X C^T, dove le V sono le matrici di covarianza
    • Linearizzazione dei casi non lineari: C diventa la matrice delle derivate.
• Lezione congiunta con il dottorato: introduzione su questioni di incertezze di misura:
  • per referenze vedi appunti della prima lezione di dottorato
  • In particolare, vedi sorgenti delle incertezze di misura ( `decalogo ISO')

 

---

Lezione 19 (20/01/11) [1 ora]

• Breve spiegazione dell'uso del regolo calcolatore
  • Importanza di interpolare!
  • Versione in java.
• Importanza del coefficiente di correlazione ρ(m,c)
  Ad esempio se trasliamo i dati lungo la x, l'errore su c varierà.
• Distribuzione normale bivariata
  (vedi dispense PRO par 9.10)
  • Caso semplice di due variabili indipendenti.
  • Caso di due variabili correlate (trattazione non rigorosa).
  • Accenno al caso generale di distribuzione multivariata.
  • Esercizio: provare a costruire con R un generatore di numeri gaussiani bivariati a partire dai seguenti valori:
    • x_medio=2.5 , σ_x=0.5
    • y_medio=1.5 , σ_y=0.5
    • nel caso di correlazione:
      • ρ= -0.8
      • ρ= 0.9
  • Soluzione (con varianti): normale_bivariata.R
• f(m,c|{x,y})
  
  • se la media delle x è nulla, f(m,c|{x,y}) si riduce al prodotto di due gaussiane, ovvero:
          f(m,c|{x,y})=f(m|{x,y})×f(c|{x,y})
         → coefficiente di correlazione fra m e c si annulla;
  • altrimenti ci si mette nel sistema traslato x'=x-x_m nel quale la media delle x' è nulla:
         E[m'], Var[m'], E[c'], Var[c'] (non correlati)
               Traslazione nel sistema originario:
                → E[m], Var[m], E[c], Var[c], Cov(m,c).

 

---

Lezione 20 (25/01/11) [1 ora]

• Esercizio: Sapendo che in LHC ci sono 10¹³protoni, e che l'energia di LHC è di 7TeV:
  
  • quanta energia cinetica hanno i protoni?
  • considerando un veicolo che viaggia a 200 km/h, che massa dovrebbe avere il veicolo affinche la sua energia cinetica sia pari a quella dei protoni?
• Incertezze di misura (nota su Errori ed incertezze di misura):
  • valore (vero), errore ed incertezza; cause delle incertezze di misura (vedi dispense pagine 8 e ss.)
  • Incertezze di tipo A e di tipo B (pag 57 e ss.)
  • Come tener conto dell'incertezza (di tipo B) dovuta agli errori sistematici più comuni:
    • errore di zero (pag 47 e ss.)
    • errore di scala (pag 49 e ss.)

[]